kjg's blog
0%

中序遍历模板 98.验证BST 99.恢复二叉树 230.BST中第K小的元素 538.把BST转化为累加树

发表于 更新于 分类于
中序遍历模板 98.验证BST(Mid) 99.恢复二叉树(Mid) 230.BST中第K小的元素(Mid) 538.把BST转化为累加树(Mid)

中序遍历模板

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> res;
    vector<int> inorderTraversal(TreeNode* root) {
        inorder(root);
        return res;
    }
    void inorder(TreeNode* root){
        if(root==nullptr) return;
        inorder(root->left);
        res.push_back(root->val);
        inorder(root->right);
    }
};

Python

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        self.res = [] # 函数内部的函数一律不加self,函数内部的变量一律加self
        def inorder(root):
            if not root: return
            inorder(root.left)
            self.res.append(root.val)
            inorder(root.right)
        inorder(root)
        return self.res

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

  • 节点的左子树只包含 小于 当前节点的数。
  • 节点的右子树只包含 大于 当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

img

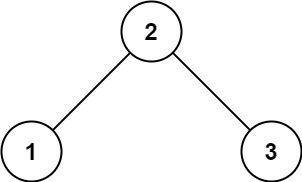
输入：root = [2,1,3]
输出：true

示例 2：

img

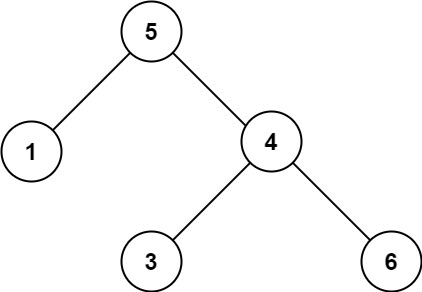
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

  • 树中节点数目范围在[1, 104] 内
  • -231 <= Node.val <= 231 - 1

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    long pre = LONG_MIN;
    bool isValidBST(TreeNode* root) {
        if(root!=nullptr){
            if(!isValidBST(root->left)) return false;
            if( root->val <=pre ) return false;
            pre = root->val;
            if(!isValidBST(root->right)) return false;
        }
        return true;
    }
};

Python

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def isValidBST(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        self.pre = float('-inf') # 最小浮点值
        def check(root):
            if root:
                if not check(root.left): return False
                if root.val <= self.pre : return False
                self.pre = root.val
                if not check(root.right): return False
            return True
        return check(root)

99. 恢复二叉搜索树

给你二叉搜索树的根节点 root ，该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树 。

示例 1：

img

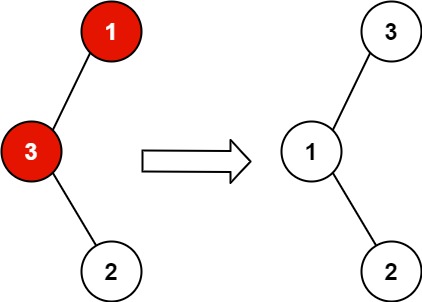
输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 的左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。

示例 2：

img

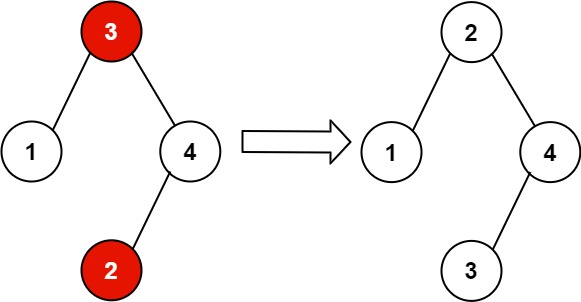
输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

提示：

  • 树上节点的数目在范围 [2, 1000] 内
  • -231 <= Node.val <= 231 - 1

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* left,* right, * pre;

    void recoverTree(TreeNode* root) {
        inorder(root);
        int temp = left->val;
        left->val = right->val;
        right->val = temp;
    }

    void inorder(TreeNode* root){
        if(root == nullptr) return;
        inorder(root->left);
        if(pre!=nullptr){
            if(pre->val>root->val){
                if(left == nullptr) left = pre;
                right = root;
            }
        }
        pre = root;
        inorder(root->right);
    }
        
};

Python

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):

    def recoverTree(self, root):
        """
        :type root: TreeNode
        :rtype: None Do not return anything, modify root in-place instead.
        """
        self.left = None
        self.right = None
        self.pre = None

        def inorder(root): # 函数内部的函数一律不加self,函数内部的变量一律加self
            if not root: return;
            inorder(root.left)
            if self.pre:
                if self.pre.val > root.val:
                    if not self.left: self.left = self.pre
                    self.right = root
            self.pre = root
            inorder(root.right)

        inorder(root)
        temp = self.left.val
        self.left.val = self.right.val
        self.right.val = temp

230. 二叉搜索树中第K小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例 1：

img

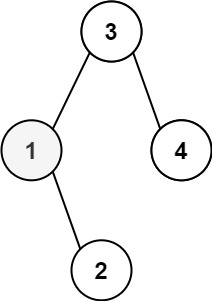
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

img

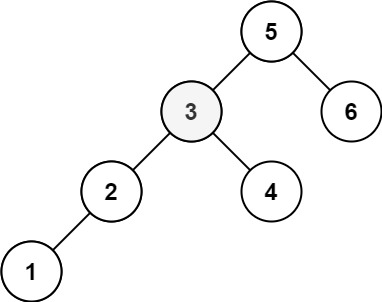
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

  • 树中的节点数为 n 。
  • 1 <= k <= n <= 104
  • 0 <= Node.val <= 104

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = 0;
    int kthSmallest(TreeNode* root, int k) {
        inorder(root,k);
        return res;
    }
    void inorder(TreeNode* root,int& k){
        if(root == nullptr) return;
        inorder(root->left,k);
        if(--k == 0) res = root->val;
        inorder(root->right,k);
    }
};

538. 把二叉搜索树转换为累加树

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

  • 节点的左子树仅包含键 小于 节点键的节点。
  • 节点的右子树仅包含键 大于 节点键的节点。
  • 左右子树也必须是二叉搜索树。

注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1：

img

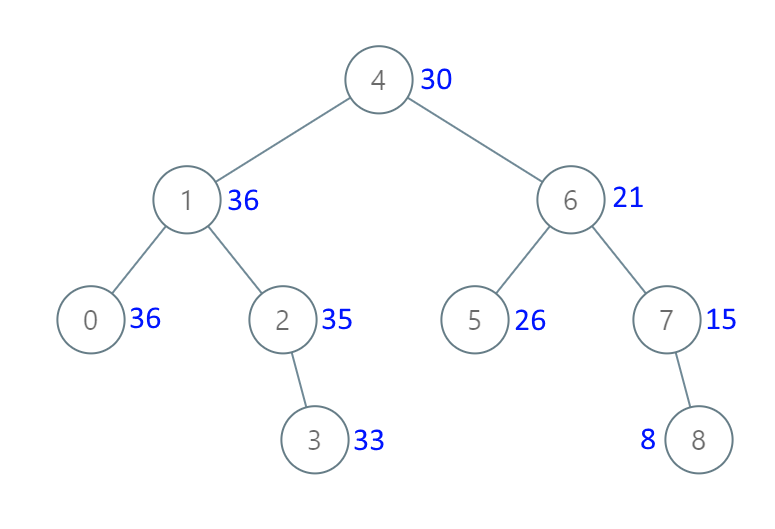
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

  • 树中的节点数介于 0 和 104 之间。
  • 每个节点的值介于 -104 和 104 之间。
  • 树中的所有值 互不相同 。
  • 给定的树为二叉搜索树。

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int accumulation = 0;
    TreeNode* convertBST(TreeNode* root) {
        iinorder(root);
        return root;
    }
    void iinorder(TreeNode* root){
        if(root == nullptr) return;
        iinorder(root->right);
        int temp = root->val;
        root->val += accumulation;
        accumulation += temp;
        iinorder(root->left);
    }
};