112.路径总和 113.路径总和II 257.二叉树的所有路径 437.路径总和III

112. 路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

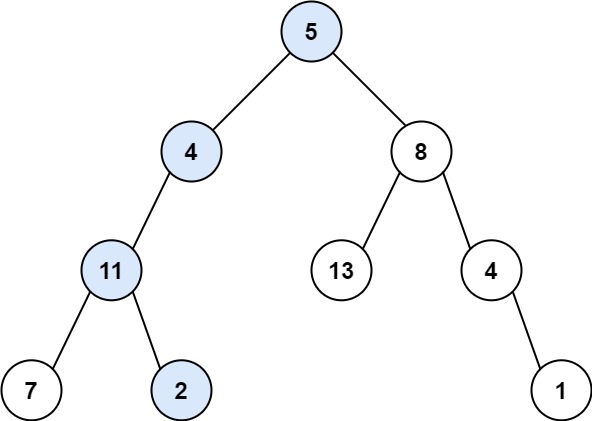
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

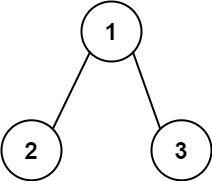
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

• 树中节点的数目在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == nullptr) return false;
        if(targetSum == root -> val && root -> left == nullptr && root -> right == nullptr) return true;
        return hasPathSum(root -> left, targetSum - root -> val) || hasPathSum(root -> right, targetSum - root -> val);
    }
};

113. 路径总和 II

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

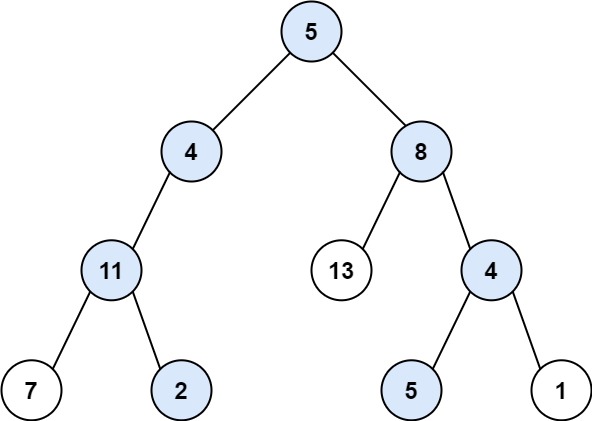
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

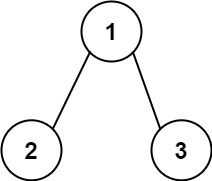
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

• 树中节点总数在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
  
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        dfs(root, targetSum);
        return res;
    }
  
    void dfs(TreeNode* root, int targetSum){
        if(root == nullptr) return;
        path.push_back(root -> val);
        targetSum -= root -> val;
        if(targetSum == 0 && root -> left == nullptr && root -> right == nullptr) res.push_back(path);
        dfs(root -> left, targetSum);
        dfs(root -> right, targetSum);
        path.pop_back();
    }
};]
  
// 等价于
class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        dfs(root, targetSum,path);
        return res;
    }
    void dfs(TreeNode* root, int targetSum, vector<int> path){
        if(root == nullptr) return;
        path.push_back(root -> val);
        targetSum -= root -> val;
        if(targetSum == 0 && root -> left == nullptr && root -> right == nullptr) res.push_back(path);
        dfs(root -> left, targetSum, path);
        dfs(root -> right, targetSum, path);
    }
};

257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

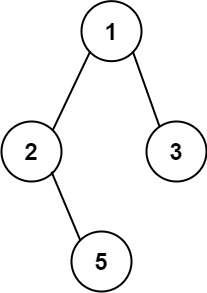
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

• 树中节点的数目在范围 [1, 100] 内
• -100 <= Node.val <= 100

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<string> res;
    string path;
    vector<string> binaryTreePaths(TreeNode* root) {
        dfs(root, res, path);
        return res;
    }
    void dfs(TreeNode* root, vector<string>& res, string path){ // & res 表示直接修改的是全局变量的那个res
        if(!root) return;
        string temp = to_string(root -> val);
        if(root -> left == nullptr && root -> right == nullptr){
            path += temp;
            res.push_back(path);
            return;
        }
        dfs(root -> left, res, path + temp + "->");
        dfs(root -> right, res, path + temp + "->");
        // path.pop_back(); 如果path作为一个形参传入dfs中就不需要这步
    }
};

437. 路径总和 III

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

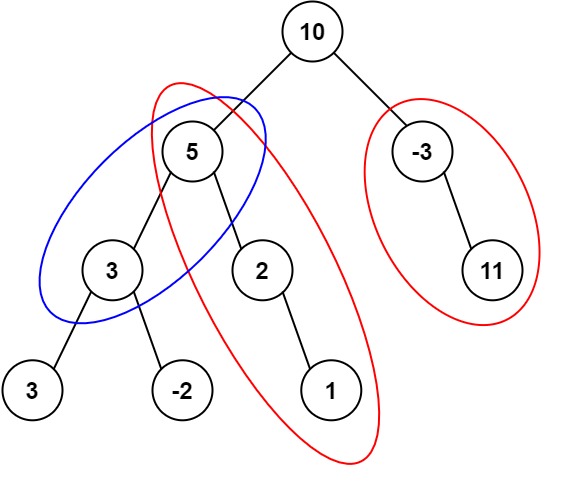
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

• 二叉树的节点个数的范围是 [0,1000]
• -109 <= Node.val <= 109
• -1000 <= targetSum <= 1000

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int cnt = 0;

    int pathSum(TreeNode* root, int targetSum) { 
        inorder(root,targetSum); //中序遍历每个节点,都做一次dfs
        return cnt;
    }

    void dfs(TreeNode* root, long sum){
        if(root == nullptr) return;
        sum -= root -> val;
        if(sum == 0) cnt++;
        dfs(root -> left, sum);
        dfs(root -> right, sum);
    }

    void inorder(TreeNode* root,long sum){ //sum 不加 & 的话 就不会变化,每次都为 targetSum
        if(!root) return;
        inorder(root -> left, sum);
        dfs(root,sum);
        inorder(root ->right, sum);
    }
};