130.被围绕的区域面试题13. 机器人的运动范围

130. 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

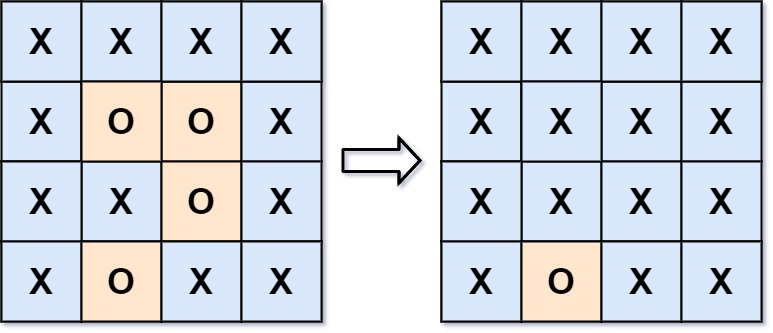
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

输入：board = [["X"]]
输出：[["X"]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 'X' 或 'O'

C++

与岛屿系列问题思路一致

class Solution {
public:
    void solve(vector<vector<char>>& board) {
        int r = board.size();
        int c = board[0].size();
        if(r == 1 || c == 1) return;
        for(int i = 0; i < r ; i++){
            for(int j = 0; j < c ; j++){
                if(board[i][j] == 'O'){
                    if(i == 0 || i == r -1 || j == c - 1|| j == 0) dfs(board, i, j);
                    // if(board[i][j] == 'O') board[i][j] = 'X'; 不能在这写是因为刚变为N后 又被变为O了，然后又被变为X了
                    // if(board[i][j] == 'N') board[i][j] = 'O'; 
                }
            }
        }
        for(int i = 0; i < r ; i++){ // N变为O O变为X
            for(int j = 0; j < c ; j++){
                if(board[i][j] == 'O') board[i][j] = 'X';
                if(board[i][j] == 'N') board[i][j] = 'O'; 
            }
        }
    }

    void dfs(vector<vector<char>>& board, int r, int c){
        if(r < 0 || r > board.size() - 1 || c < 0 || c > board[0].size() - 1) return;
        if(board[r][c] != 'O') return;
        board[r][c] = 'N'; // 先遍历边界的O,将与之相连的O全改成N 
        dfs(board, r + 1, c);
        dfs(board, r - 1, c);
        dfs(board, r, c + 1);
        dfs(board, r, c - 1);
    }
  
};

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：

输入：m = 2, n = 3, k = 1
输出：3

示例 2：

输入：m = 3, n = 1, k = 0
输出：1

提示：

1 <= n,m <= 100
0 <= k <= 20

C++

与岛屿系列问题思路一致

class Solution {
public:
    int res = 0;
    int movingCount(int m, int n, int k) {
        vector<vector<int>> visited(m, vector<int>(n, 0)); // 初始化为m行n列的0
        dfs(m, n, 0, 0, k, visited);
        return res;
    }
    void dfs(int m, int n, int r, int c, int k, vector<vector<int>>& visited){
        if(r < 0 || r > m - 1 || c < 0 || c > n - 1) return;
        if((r % 10 + r / 10 + c % 10 + c / 10) > k) return;
        if(visited[r][c] != 0) return; // 已经被访问过
        visited[r][c] = 1;
        res ++;
        dfs(m, n, r + 1, c, k, visited);
        dfs(m, n, r - 1, c, k, visited);
        dfs(m, n, r , c + 1, k, visited);
        dfs(m, n, r , c - 1, k, visited);
    } 
};