给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
返回 3 , 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意: 两结点之间的路径长度是以它们之间边的数目表示。
C++ class Solution {public : int res = 0 ; int diameterOfBinaryTree (TreeNode* root) dfs (root); return res; } int maxHeight (TreeNode* root) if (!root) return 0 ; return max (maxHeight (root -> left), maxHeight (root -> right)) + 1 ; } void dfs (TreeNode* root) if (!root) return ; dfs (root -> left); res = max ((maxHeight (root -> left) + maxHeight (root -> right) ), res); dfs (root -> right); } };
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例 1:
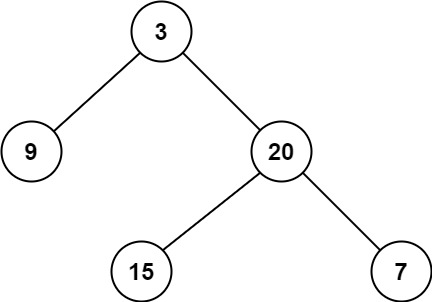
输入:root = [3 ,9 ,20 ,null ,null ,15 ,7 ] 输出:2
示例 2:
输入:root = [2 ,null ,3 ,null ,4 ,null ,5 ,null ,6 ] 输出:5
提示:
树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000
C++ class Solution {public : int minDepth (TreeNode* root) if (!root) return 0 ; if (!root -> left) return minDepth (root -> right) + 1 ; if (!root -> right) return minDepth (root -> left) + 1 ; return min (minDepth (root -> left), minDepth (root -> right)) + 1 ; } };
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: [3,9,20,null,null,15,7],
返回它的最大深度 3 。
C++ class Solution {public : int maxDepth (TreeNode* root) if (!root) return 0 ; return max (maxDepth (root -> left), maxDepth (root -> right)) + 1 ; } };
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同,但 父节点不同 ,则它们是一对堂兄弟节点 。
我们给出了具有唯一值的二叉树的根节点 root ,以及树中两个不同节点的值 x 和 y 。
只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true 。否则,返回 false。
示例 1:
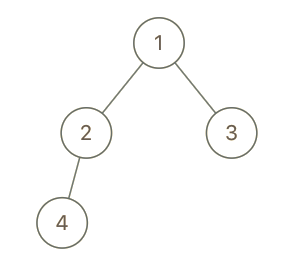
输入:root = [1 , 2 , 3 , 4 ], x = 4 , y = 3 输出:false
示例 2:
输入:root = [1 , 2 , 3 , null , 4 , null , 5 ], x = 5 , y = 4 输出:true
示例 3:
输入:root = [1 , 2 , 3 , null , 4 ], x = 2 , y = 3 输出:false
提示:
二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。
C++ class Solution {private : int x_depth = 0 ; int y_depth = 0 ; public : bool isCousins (TreeNode* root, int x, int y) dfs (root, x, y, 0 ); if (x_depth == y_depth){ return !isBrother (root, x, y); } return false ; } void dfs (TreeNode* root, int x, int y, int depth) if (!root) return ; if (root -> val == x) x_depth = depth; if (root -> val == y) y_depth = depth; dfs (root -> left, x, y, depth + 1 ); dfs (root -> right, x, y, depth + 1 ); } bool isBrother (TreeNode* root, int x, int y) if (!root) return false ; if ( root -> left && root -> right){ if (root -> left -> val == x && root -> right -> val == y) return true ; if (root -> left -> val == y && root -> right -> val == x) return true ; } return isBrother (root -> left, x, y) || isBrother (root -> right, x, y); } };
给你一个二叉树的根节点 root ,计算并返回 整个树 的坡度 。
一个树的 节点的坡度 定义即为,该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话,左子树的节点之和为 0 ;没有右子树的话也是一样。空结点的坡度是 0 。
整个树 的坡度就是其所有节点的坡度之和。
示例 1:
输入:root = [1,2,3] 输出:1 解释: 节点 2 的坡度:|0-0| = 0(没有子节点) 节点 3 的坡度:|0-0| = 0(没有子节点) 节点 1 的坡度:|2-3| = 1(左子树就是左子节点,所以和是 2 ;右子树就是右子节点,所以和是 3 ) 坡度总和:0 + 0 + 1 = 1
示例 2:
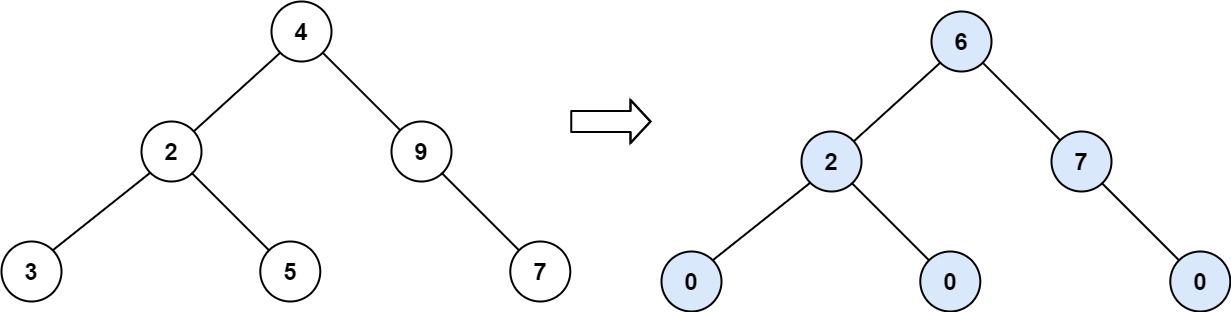
输入:root = [4,2,9,3,5,null,7] 输出:15 解释: 节点 3 的坡度:|0-0| = 0(没有子节点) 节点 5 的坡度:|0-0| = 0(没有子节点) 节点 7 的坡度:|0-0| = 0(没有子节点) 节点 2 的坡度:|3-5| = 2(左子树就是左子节点,所以和是 3 ;右子树就是右子节点,所以和是 5 ) 节点 9 的坡度:|0-7| = 7(没有左子树,所以和是 0 ;右子树正好是右子节点,所以和是 7 ) 节点 4 的坡度:|(3+5+2)-(9+7)| = |10-16| = 6(左子树值为 3、5 和 2 ,和是 10 ;右子树值为 9 和 7 ,和是 16 ) 坡度总和:0 + 0 + 0 + 2 + 7 + 6 = 15
示例 3:
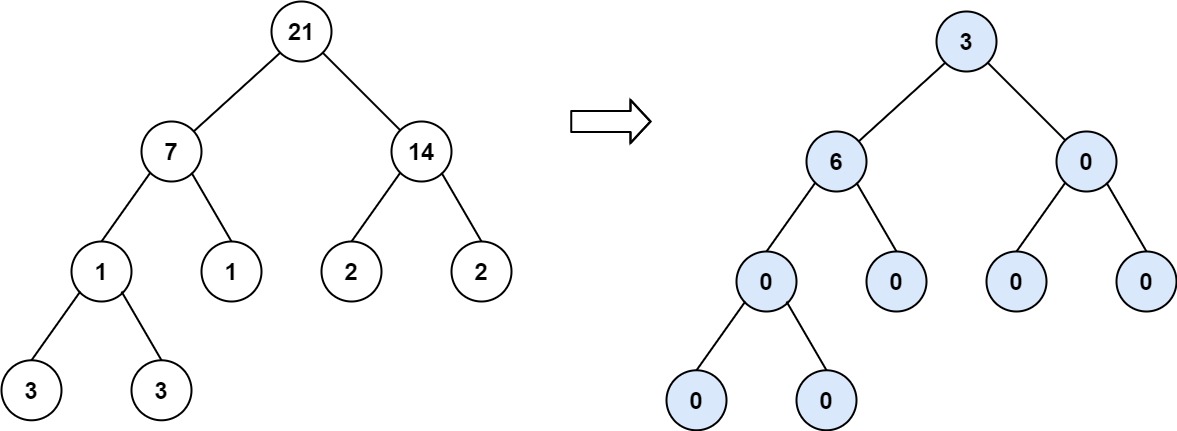
输入:root = [21,7,14,1 ,1,2,2,3 ,3 ] 输出:9
提示:
树中节点数目的范围在 [0, 104] 内
-1000 <= Node.val <= 1000
C++ class Solution {public : int res = 0 ; int findTilt (TreeNode* root) dfs (root); return res; } int dfs (TreeNode* root) if (!root) return 0 ; int l = dfs (root -> left); int r = dfs (root -> right); res += abs (l -r); return root -> val + l + r; } };
给定一个二叉树,判断它是否是高度平衡的二叉树。
提示:
树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104
C++ class Solution {public : bool isBalanced (TreeNode* root) if (!root) return true ; int lh = height (root -> left); int rh = height (root -> right); return abs (lh - rh) <= 1 && isBalanced (root -> left) && isBalanced (root -> right); } int height (TreeNode* root) if (!root) return 0 ; return max (height (root -> left), height (root -> right)) + 1 ; } };
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
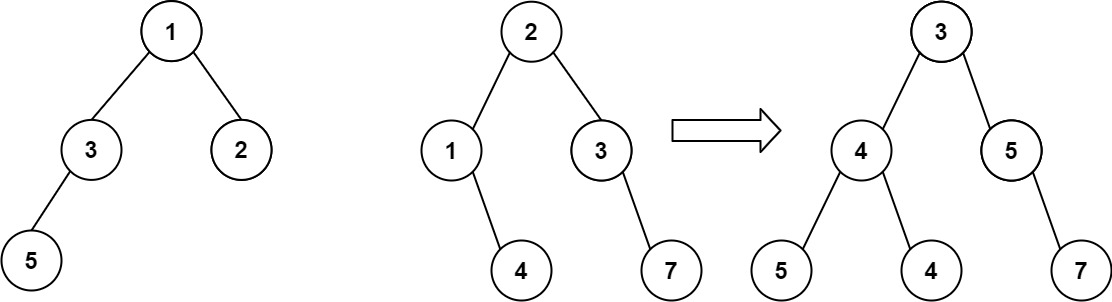
输入:root1 = [1 ,3 ,2 ,5 ], root2 = [2 ,1 ,3 ,null ,4 ,null ,7 ] 输出:[3 ,4 ,5 ,5 ,4 ,null ,7 ]
示例 2:
提示:
两棵树中的节点数目在范围 [0, 2000] 内
-104 <= Node.val <= 104
C++ class Solution {public : TreeNode* root = nullptr ; TreeNode* mergeTrees (TreeNode* root1, TreeNode* root2) { if (!root1 && !root2) return nullptr ; if (!root1) return root2; if (!root2) return root1; TreeNode* root = new TreeNode (root1 -> val + root2 -> val); root -> left = mergeTrees (root1 -> left, root2 -> left); root -> right = mergeTrees (root1 -> right, root2 -> right); return root; } };
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
C++ class Solution {public : TreeNode* invertTree (TreeNode* root) { if (!root) return nullptr ; dfs (root); return root; } void dfs (TreeNode* root) if (!root || (!root -> left && !root -> right)) return ; else { TreeNode* temp = root ->left; root ->left = root -> right; root -> right = temp; } dfs (root -> left); dfs (root -> right); } };
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
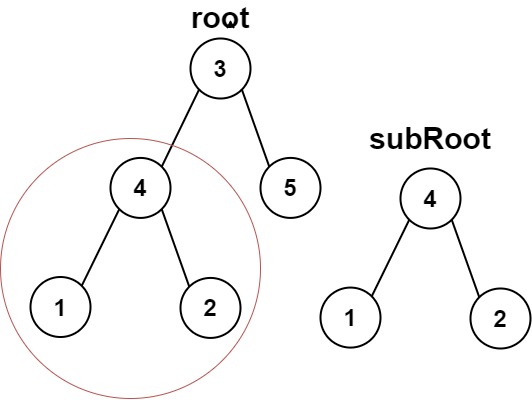
示例 1:
输入:root = , subRoot = 输出:true
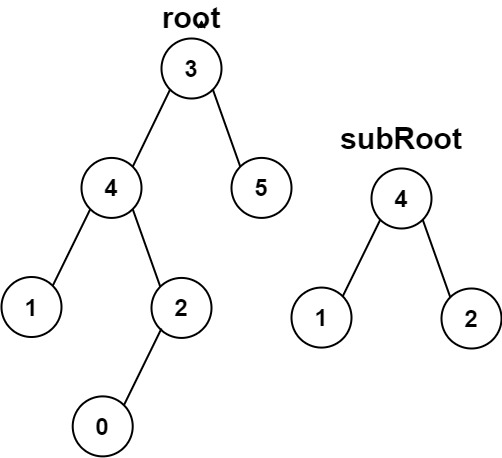
示例 2:
输入:root = [3 ,4 ,5 ,1 ,2 ,null ,null ,null ,null ,0 ], subRoot = [4 ,1 ,2 ] 输出:false
提示:
root 树上的节点数量范围是 [1, 2000]subRoot 树上的节点数量范围是 [1, 1000]-104 <= root.val <= 104-104 <= subRoot.val <= 104
C++ class Solution {public : bool tag = false ; bool isSubtree (TreeNode* root, TreeNode* subRoot) dfs (root, subRoot); return tag; } bool isSametree (TreeNode* root1, TreeNode* root2) if (!root1 && !root2) return true ; if ((!root1 && root2) || (root1 && !root2) || root1 -> val != root2 -> val) return false ; return isSametree (root1 -> left, root2 -> left) && isSametree (root1 -> right, root2 -> right); return true ; } void dfs (TreeNode* root, TreeNode* subRoot) if (!root) return ; if (root -> val == subRoot -> val){ if (tag == true ) return ; tag = isSametree (root -> left, subRoot -> left) && isSametree (root -> right, subRoot -> right); } dfs (root -> left, subRoot); dfs (root -> right, subRoot); } };