662.二叉树最大宽度

662. 二叉树最大宽度

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

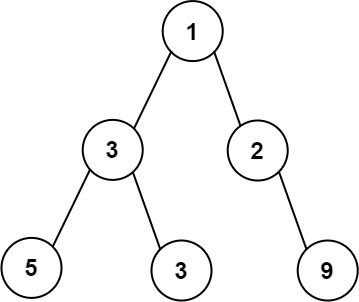
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

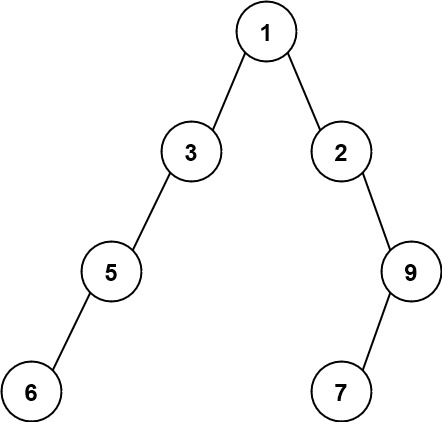
输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

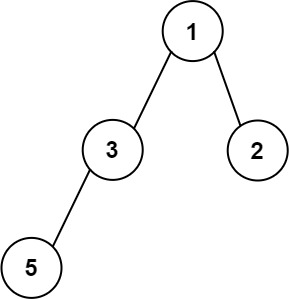
输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

提示：

• 树中节点的数目范围是 [1, 3000]
• -100 <= Node.val <= 100

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = 0;

    int widthOfBinaryTree(TreeNode* root) {
        vector<int> left; // 存放每层最左边不为空的节点index
        dfs(root, 1, 1, left);
        return res;
    }

    void dfs(TreeNode* root, int lvl, unsigned int index, vector<int>& left){
        if(!root) return;
        if(lvl > left.size()) left.push_back(index);  // 如果lvl > left.size()说明当前节点就是新的一层的最左节点
        res = res > index - left[lvl - 1] + 1 ? res : index - left[lvl - 1] + 1 ;  
        dfs(root -> left, lvl + 1, index * 2, left);
        dfs(root -> right, lvl + 1, index * 2 + 1, left);
    }
};