797.所有可能的路径

797. 所有可能的路径

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

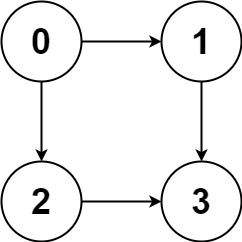
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

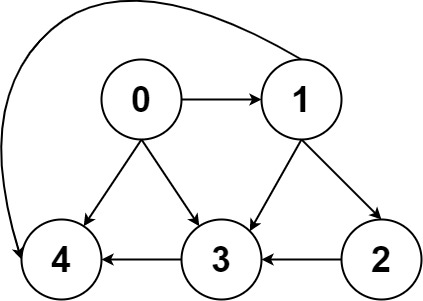
提示：

• n == graph.length
• 2 <= n <= 15
• 0 <= graph[i][j] < n
• graph[i][j] != i（即不存在自环）
• graph[i] 中的所有元素 互不相同
• 保证输入为 有向无环图（DAG）

C++

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;

    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        dfs(0, graph.size() - 1, path, graph);
        return res;
    }

    void dfs(int start, int end, vector<int> path, vector<vector<int>>& graph){
        if(start == end){
            path.push_back(end);
            res.push_back(path);
            return;    
        }
        if(graph[start].empty()) return;

        path.push_back(start);
        for(auto elem : graph[start]){
            dfs(elem, end, path, graph);
        }
    }
};