回溯之组合总和合集

递归、回溯、DFS的区别

递归是一种算法结构，DFS是一种搜索（方法）工具，回溯是一种算法思想

1. 在函数中调用函数本身来解决子问题以达到解决原问题的方法就叫递归

   对于一个可以分解的问题，子问题与原问题处理过程完全相同，区别只在于数据规模，可以用递归来解

2. 回溯就是通过不同的尝试来搜索问题的解

   有点类似于穷举（搜索全部解空间），但是和穷举不同的是回溯会“剪枝”，对已经知道错误的结果没必要再枚举接下来的答案了

3. 回溯搜索是深度优先搜索（DFS）的一种情况

   对于某一个搜索树来说（搜索树是起记录路径和状态判断的作用），回溯和DFS，其主要的区别是，回溯法在求解过程中不保留完整的树结构（剪枝），而深度优先搜索则记下完整的搜索树

   在深度优先搜索中，用标志的方法记录访问过的状态，这种处理方法使得深度优先搜索法与回溯法没什么区别了

回溯模板

void backtracking(参数) {
    if (终止条件) {
        收集结果;
        return;
    }
    for (该节点的所有子节点){
        处理结点;
        递归函数;
        回溯操作（比如 收集结果12 撤销2,收集结果13 撤销3）;
    }
}

39. 组合总和

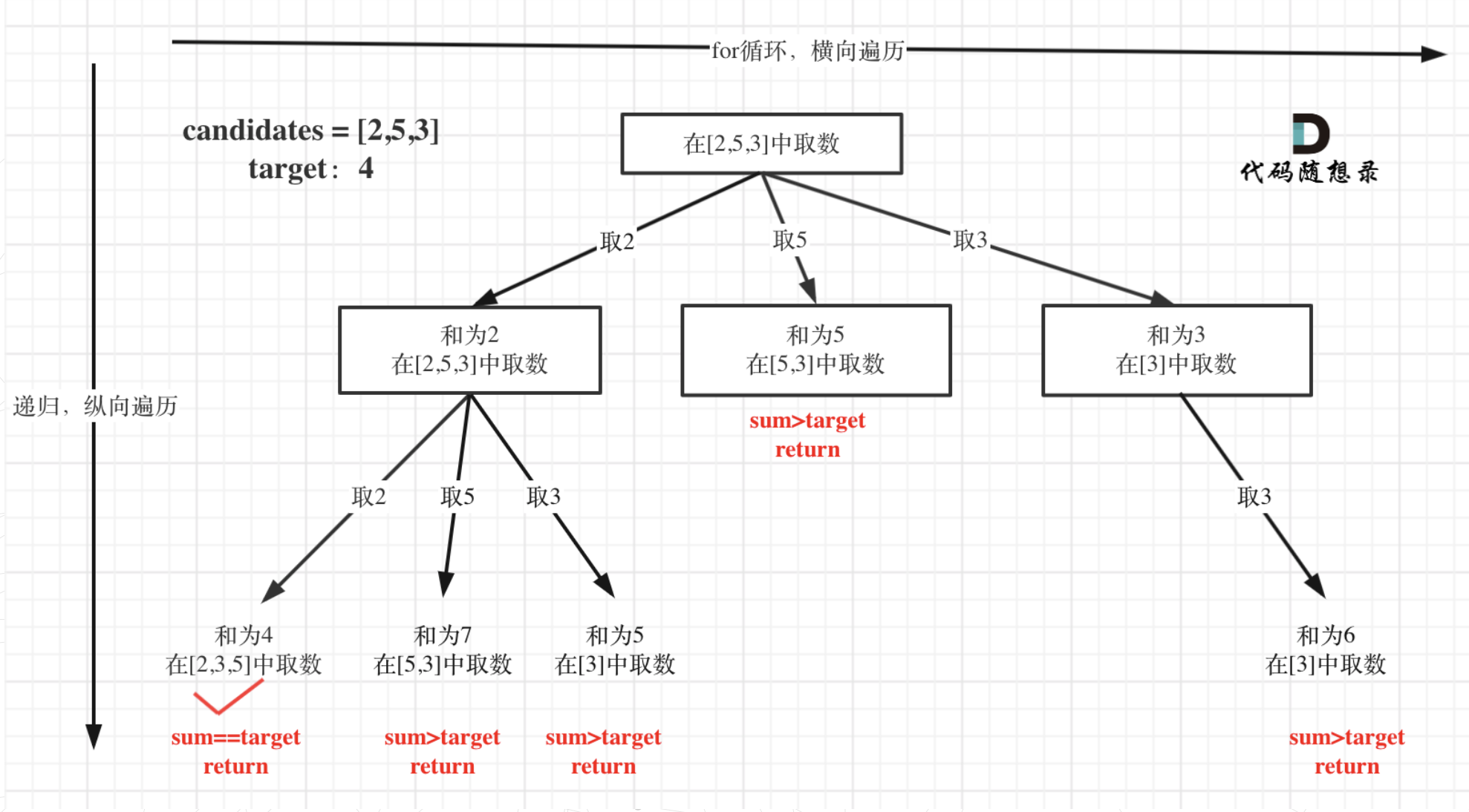
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

• 1 <= candidates.length <= 30
• 2 <= candidates[i] <= 40
• candidates 的所有元素 互不相同
• 1 <= target <= 40

C++

• 回溯无剪枝

// 版本一
class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
        if (sum > target) return;
        if (sum == target) {
            result.push_back(path);
            return;
        }

        for (int i = startIndex; i < candidates.size(); i++) {
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i); // 不用i+1了，表示可以重复读取当前的数
            sum -= candidates[i];
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backtracking(candidates, target, 0, 0);
        return result;
    }
};

• 回溯有剪枝

上面的版本一的代码可以看到，对于sum已经大于target的情况，其实是依然进入了下一层递归，只是下一层递归结束判断的时候，会判断sum > target的话就返回。

其实如果已经知道下一层的sum会大于target，就没有必要进入下一层递归了。

那么可以在for循环的搜索范围上做做文章了。

对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历。

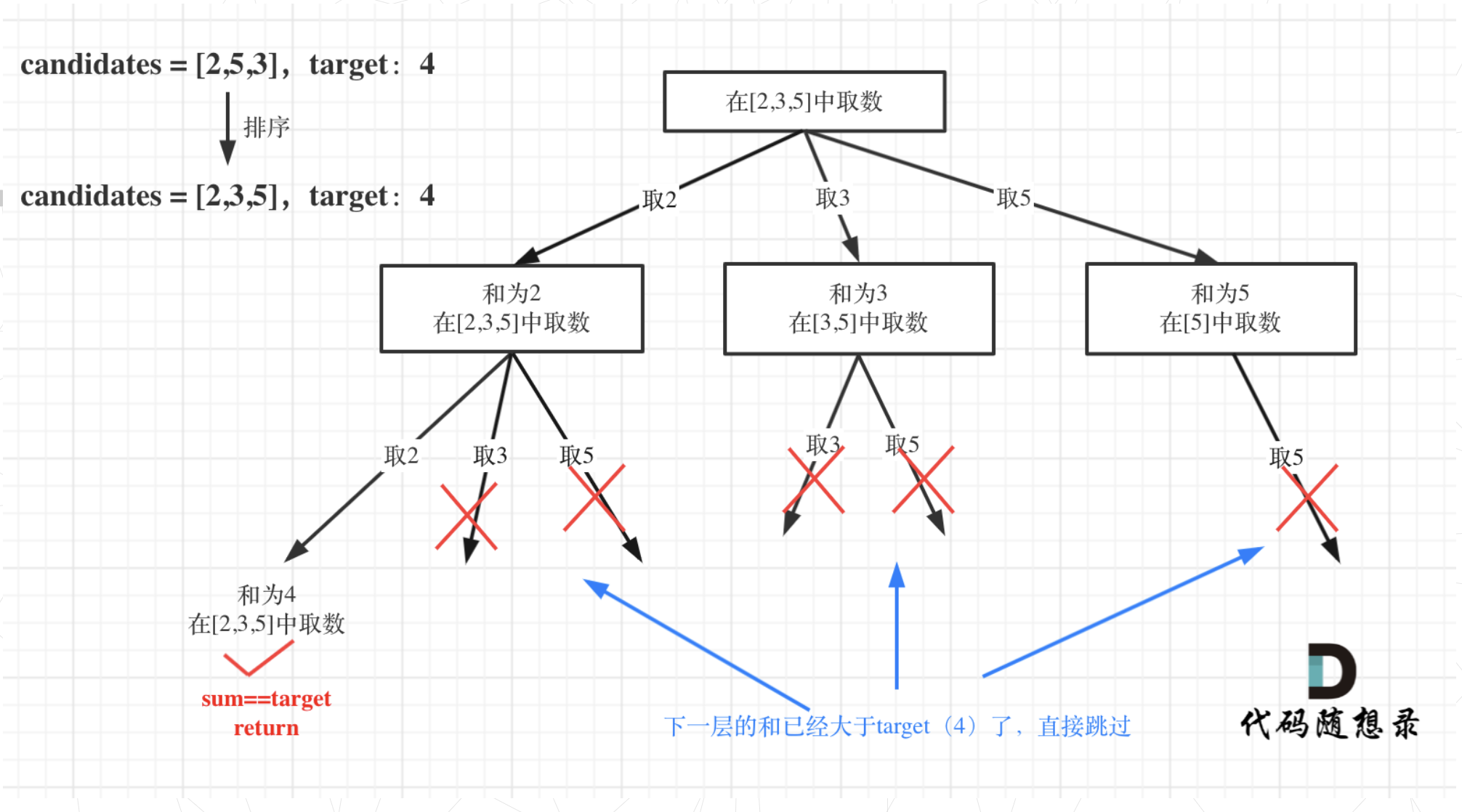
class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
        if (sum == target) {
            result.push_back(path);
            return;
        }

        // 如果 sum + candidates[i] > target 就终止遍历
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i);
            sum -= candidates[i];
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end()); // 需要排序
        backtracking(candidates, target, 0, 0);
        return result;
    }
};

• 其他思路

// 思路二：正确, 每个idx都有选或者不选两种情况
class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        dfs(0, candidates, target, path);
        return res;
    }

    void dfs(int idx,vector<int>& candidates, int target, vector<int> path){
        if(idx == candidates.size() || target < 0) return;
        if(target == 0) {
            res.push_back(path);
            return;
        }

        dfs(idx + 1, candidates, target, path); // 要在前, 因为跳过的话, target不能减少

        path.push_back(candidates[idx]);
        dfs(idx, candidates, target - candidates[idx], path);
    }
};

// 错误版本:把它想成了根节点为0的四叉树
// 输入 [2,3,6,7] 7
// 输出 [[0,2,2,3],[0,2,3,2],[0,3,2,2],[0,7]]
// 预期结果 [[2,2,3],[7]]
class Solution {
public:
    vector<vector<int>> res;
    set<vector<int>> st;
    vector<int> path;
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        dfs(0, candidates, target, path);
        for(auto elem : st){
            res.push_back(elem);
        }
        return res;
    }

    void dfs(int cur, vector<int>& candidates, int target, vector<int> path){
        if(target < 0) return;
        if(target == 0) st.insert(path);
        target = target - cur;
        path.push_back(cur);
        for(auto elem : candidates){
            dfs(elem, candidates, target, path);
        }
    }
};

40. 组合总和 II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

• 1 <= candidates.length <= 100
• 1 <= candidates[i] <= 50
• 1 <= target <= 30

C++

避免重复思想：
这个方法最重要的作用是，可以让同一层级，不出现相同的元素。即
                  1
                 / \
                2   2  这种情况不会发生 但是却允许了不同层级之间的重复即：
               /     \
              5       5
                例2
                  1
                 /
                2      这种情况确是允许的
               /
              2  

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target){
        sort(candidates.begin(), candidates.end());
        backtracking(candidates, target, 0, 0);
        return res;
    }

    void backtracking(vector<int>& candidates, int target, int sum, int startIndex){
        if(sum == target){
            res.push_back(path);
            return;
        }

        for(int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i ++){
            if(i > startIndex && candidates[i] == candidates[i -1]) continue; // 见上图
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i + 1);
            sum -= candidates[i];
            path.pop_back();
        }
    }
};

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

C++

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return res;
    }

    void backtracking(int n, int k, int startIdx){
        if(path.size() == k){
            res.push_back(path);
            return;
        }

        for(int i = startIdx; i <= n; i ++){
            path.push_back(i);
            backtracking(n, k, i + 1);
            path.pop_back();
        }
    }
};

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

C++

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path = {};
    vector<vector<int>> subsets(vector<int>& nums) {
        for(int i = 0; i <= nums.size(); i ++){ // 分别将长度为0， 1， 2，... 的子集求出
            backtracking(nums, 0, i);
        }
        return res;
    }

    void backtracking(vector<int>& nums, int startIdx, int cnt){
        if(path.size() == cnt){
            res.push_back(path);
            return;
        }

        for(int i = startIdx; i < nums.size(); i ++){
            path.push_back(nums[i]);    
            backtracking(nums, i + 1, cnt);
            path.pop_back();
        }
    }
};

90. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10

C++

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path = {};
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(), nums.end());  // 必须要排序，不然 nums[i] == nums[i - 1] 不起效果
        for(int i = 0; i <= nums.size(); i ++){
            backtracking(nums, 0, i);
        }
        return res;
    }

    void backtracking(vector<int>& nums, int startIdx, int cnt){
        if(path.size() == cnt){
            res.push_back(path);
            return;
        }

        for(int i = startIdx; i < nums.size(); i ++){
            if(i > startIdx && nums[i] == nums[i - 1]) continue;
            path.push_back(nums[i]);    
            backtracking(nums, i + 1, cnt);
            path.pop_back();
        }
    }
};

784. 字母大小写全排列

给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。

返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。

示例 1：

输入：s = "a1b2"
输出：["a1b2", "a1B2", "A1b2", "A1B2"]

示例 2:

输入: s = "3z4"
输出: ["3z4","3Z4"]

提示:

• 1 <= s.length <= 12
• s 由小写英文字母、大写英文字母和数字组成

C++

class Solution {
public:
    vector<string> res;
    vector<string> letterCasePermutation(string s) {
        backtracking(s,0);
        return res;
    }
    void backtracking(string s, int idx){
        res.push_back(s);
        for(int i = idx; i < s.size(); i++){
            if('0'<=s[i]&&s[i]<='9') continue;
            else{
                s[i] = s[i] ^ 32;
                backtracking(s,i+1);
                s[i] = s[i] ^ 32;
            }
        }
    }
};