力扣第319场周赛

2470. 最小公倍数为 K 的子数组数目

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 nums 的 子数组 中满足 元素最小公倍数为 k 的子数组数目。

子数组 是数组中一个连续非空的元素序列。

数组的最小公倍数 是可被所有数组元素整除的最小正整数。

示例 1 ：

输入：nums = [3,6,2,7,1], k = 6
输出：4
解释：以 6 为最小公倍数的子数组是：
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]

示例 2 ：

输入：nums = [3], k = 2
输出：0
解释：不存在以 2 为最小公倍数的子数组。

提示：

1 <= nums.length <= 1000
1 <= nums[i], k <= 1000

C++

最大公约数模板

int gcd(int a,int b){
    return b? gcd(b, a% b) : a;
}

题解

class Solution {
public:
    int gcd(int a,int b){
        return b? gcd(b, a% b) : a;
    }

    int subarrayLCM(vector<int>& nums, int k) {
        int res = 0;
        for(int i = 0; i < nums.size(); i ++){
            int tmp = nums[i]; // 最小公倍数， 一开始是自己
            for(int j = i; j < nums.size(); j ++){
                tmp = tmp * nums[j]/ gcd(tmp, nums[j]); // 最小公倍数 [a,b] =  a * b / (a,b) 最大公约数
                if(tmp == k) res ++;
                if(tmp > k) break;
            }
        }
        return res;
    }
};

2471. 逐层排序二叉树所需的最少操作数目

给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的层数是该节点和根节点之间的路径的边数。

示例 1 ：

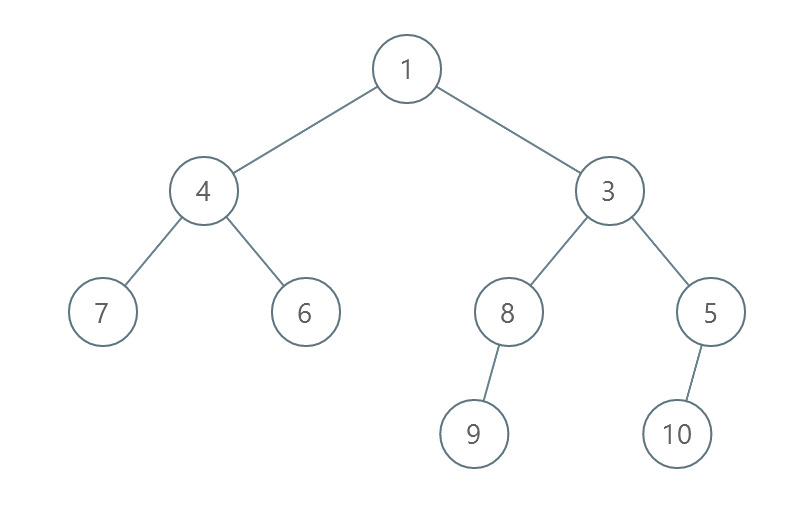
输入：root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出：3
解释：
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作，所以返回 3 。
可以证明 3 是需要的最少操作数目。

提示：

树中节点的数目在范围 [1, 105] 。
1 <= Node.val <= 105
树中的所有值 互不相同 。

C++

置换环：现在是两个环，若想要把原数组变成升序，则最少需要交换（数组长度 - 环数）次

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 并查集数组
    vector<int> v;
    int find(int x){
        if(v[x]!= x) v[x] = find(v[x]);
        return v[x];
    }

    int minimumOperations(TreeNode* root) {

        vector<int> nodes,ls; // nodes存放所有层结点值, ls存放每层的节点数
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty()){
            int n = q.size();
            ls.push_back(n);
            for(int i = 0; i< n; i ++){
                auto t = q.front();
                nodes.push_back(t ->val);
                q.pop();
                if(t -> left) q.push(t -> left);
                if(t-> right) q.push(t -> right);
            }
        }

        unordered_map <int, int> pos; // pos[i]为 i 在每层未排序之前的的位置
        for(int i = 0; i < nodes.size(); i ++){
            pos[nodes[i]] = i;
            v.push_back(i); // 初始化并查集
        }

        auto begin = nodes.begin();
        for(int i = 0; i < ls.size(); i ++){
            sort(begin, begin + ls[i]);
            begin = begin + ls[i];
        }

        int cnt = nodes.size();
        for(int i = 0; i < nodes.size(); i ++ ) {
            // 排序前[1, 4,3, 7,6,8,5, 9,10]  pos[4] = 1  v[1] = 1 
            // 排序后[1, 3,4, 5,6,7,8, 9,10]  
            int a = find(i), b = find(pos[nodes[i]]);  // i是排序完的位置, pos[nodes[i]]是未排序的位置
            if (a != b) {
                v[a] = b;
                cnt -- ;
            }
        }

        return nodes.size() - cnt;
    }
};

2472. 不重叠回文子字符串的最大数目

给你一个字符串 s 和一个正整数 k 。

从字符串 s 中选出一组满足下述条件且 不重叠 的子字符串：

每个子字符串的长度至少为 k 。
每个子字符串是一个 回文串 。

返回最优方案中能选择的子字符串的最大数目。

子字符串 是字符串中一个连续的字符序列。

示例 1 ：

输入：s = "abaccdbbd", k = 3
输出：2
解释：可以选择 s = "abaccdbbd" 中斜体加粗的子字符串。"aba" 和 "dbbd" 都是回文，且长度至少为 k = 3 。
可以证明，无法选出两个以上的有效子字符串。

示例 2 ：

输入：s = "adbcda", k = 2
输出：0
解释：字符串中不存在长度至少为 2 的回文子字符串。

提示：

1 <= k <= s.length <= 2000
s 仅由小写英文字母组成

C++

class Solution {
public:
    int maxPalindromes(string s, int k) {
        int n = s.size();
        vector<vector<bool>> g(n + 1, vector<bool>(n + 1));
        for (int len = 1; len <= n; len ++ ) {
            for (int i = 1; i + len - 1 <= n; i ++ ) {
                int j = i + len - 1;
                if (s[i - 1] == s[j - 1] && (len <= 2 || g[i + 1][j - 1]))
                    g[i][j] = true;
            }
        } // g[i][j] = true 表示的是原数组第i个到第j个字符组成回文子串;  区别于下标i,j

        vector<int> f(n + 1);
        for (int i = 1; i <= n; i ++ ) {
            f[i] = f[i - 1];
            for (int j = i - k; j >= 0; j -- ) {
                if (g[j + 1][i]) {
                    f[i] = max(f[i], f[j] + 1);
                }
            }
        }

        return f[n];
    }
};