DP之0-1背包合集

0-1背包模板

背包最大重量为4。

有三个物品	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

二维数组版

dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少

初始化

// 倒叙遍历
for (int j = bagWeight; j >= weight[0]; j--) { // j从最大容量开始，直到j不小于下标为i的物品的容量
    dp[0][j] = dp[0][j - weight[0]] + value[0]; // 初始化i为0时候的情况
}

但如果一旦正序遍历了，那么物品0就会被重复加入多次！例如代码如下：

// 正序遍历
for (int j = weight[0]; j <= bagWeight; j++) {
    dp[0][j] = dp[0][j - weight[0]] + value[0];
}
// 例如dp[0][1] 是15，到了dp[0][2] = dp[0][2 - 1] + 15; 也就是dp[0][2] = 30 了，那么就是物品0被重复放入了。

模板

void main() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;

    // 初始化
    vector<vector<int>> dp(weight.size(), vector<int>(bagWeight + 1, 0));
    for (int j = bagWeight; j >= weight[0]; j--) {
        dp[0][j] = dp[0][j - weight[0]] + value[0];
    }

    // weight数组的大小 就是物品个数
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        }
    }
    cout << dp[weight.size() - 1][bagWeight] << endl;
}

或者

void main() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;

    // 初始化
    vector<vector<int>> dp(weight.size() + 1, vector<int>(bagWeight + 1, 0));

    // weight数组的大小 就是物品个数
    for(int i = 1; i <= weight.size(); i++) { // 遍历物品
        for(int j = 1; j <= bagWeight; j++) { // 遍历背包容量
            if (j < weight[i - 1]) dp[i][j] = dp[i - 1][j]; // 包里容量不够了
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
        }
    }
    cout << dp[weight.size()][bagWeight] << endl;
}

一维数组版

在使用二维数组时:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]

dp[j]可以通过dp[j - weight[j]]推导出来，dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

初始化

dp[0] = 0;
// 如果题目给的价值都是正整数那么非0下标都初始化为0就可以了
// 如果题目给的价值有负数，那么非0下标就要初始化为负无穷

模板

二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小

void main() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;

    // 初始化
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品,每遍历到一个新元素,就更新dp数组
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}

若正序遍历背包容量:

物品0的重量weight[0] = 1，价值value[0] = 15

dp[1] = dp[1 - weight[0]] + value[0] = 15

dp[2] = dp[2 - weight[0]] + value[0] = 30

此时dp[2]就已经是30了，意味着物品0，被放入了两次，所以不能正序遍历。

为什么倒叙遍历，就可以保证物品只放入一次呢？

倒叙就是先算dp[2]

dp[2] = dp[2 - weight[0]] + value[0] = 15 （dp数组已经都初始化为0）

dp[1] = dp[1 - weight[0]] + value[0] = 15

所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了

416. 分割等和子集

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

C++

// d(i, s) : 是否存在：nums区间[0, i] 中取一些元素，使其和为s
// d(i, s) = d(i-1, s)【 不取nums[i]】 || d(i-1, s-nums[i])【 取nums[i]】

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for(auto elem: nums) sum+= elem;
        if(sum % 2) return false;

        int halfSum = sum / 2;
        return func(nums, halfSum);
    }

    bool func(vector<int>& nums, int k){ // 判断数组nums是否有和为k的子集
        // dp[i][k - 1]表示是否在 nums下标的0-i里存在和为k的子集
        vector<vector<bool>> dp (nums.size(), vector<bool>(k, false)); 
        if(nums[0] <= k) dp[0][nums[0] - 1] = true;

        // 我们求dp第i行的时候dp[i][?]，我们只需要知道dp的i-1行即可dp[i-1][?];
        // 也就是说，按照这个依赖关系，一直往下递推，只要得到第0行即可。
        for(int i = 1; i < nums.size(); i ++){
            for(int j = 0; j < k; j ++){
                //  不取nums[i] || 取nums[i]
                dp[i][j] = dp[i - 1][j] || ((j - nums[i] >=0) ? dp[i - 1][j - nums[i]] : false);  
            }
        }
        return dp[nums.size() - 1][k - 1];
    }
};

1046. 最后一块石头的重量

有一堆石头，每块石头的重量都是正整数。

每一回合，从中选出两块 最重的 石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块石头。返回此石头的重量。如果没有石头剩下，就返回 0。

示例：

输入：[2,7,4,1,8,1]
输出：1
解释：
先选出 7 和 8，得到 1，所以数组转换为 [2,4,1,1,1]，
再选出 2 和 4，得到 2，所以数组转换为 [2,1,1,1]，
接着是 2 和 1，得到 1，所以数组转换为 [1,1,1]，
最后选出 1 和 1，得到 0，最终数组转换为 [1]，这就是最后剩下那块石头的重量。

提示：

• 1 <= stones.length <= 30
• 1 <= stones[i] <= 1000

C++

• 优先队列

class Solution {
public:
    int lastStoneWeight(vector<int>& stones) {
        priority_queue<int> q;
        for (int s: stones) {
            q.push(s);
        }

        while (q.size() > 1) {
            int a = q.top();
            q.pop();
            int b = q.top();
            q.pop();
            if (a > b) {
                q.push(a - b);
            }
        }
        return q.empty() ? 0 : q.top();
    }
};

1049. 最后一块石头的重量 II

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

示例 1：

输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例 2：

输入：stones = [31,26,33,21,40]
输出：5

提示：

• 1 <= stones.length <= 30
• 1 <= stones[i] <= 100

C++

/* 0-1背包问题
问题转化为：把一堆石头分成两堆,求两堆石头重量差最小值
进一步分析：要让差值小,两堆石头的重量都要接近sum/2;我们假设两堆分别为A,B,A<sum/2,B>sum/2,若A更接近sum/2,B也相应更接近sum/2
进一步转化：将一堆stone放进最大容量为sum/2的背包,求放进去的石头的最大重量MaxWeight,最终答案即为sum-2*MaxWeight;
*/
class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        int n = stones.size();
        int sum = 0;
        for(int t : stones) sum += t;
        int target = sum / 2; // 背包容量：target 求放进去的物品的最大重量MaxWeight
        // dp[i][j]含义:从前i块石头中选取，选取值之和小于等于目标值j的最大值
        vector<vector<int>> dp(n + 1, vector<int>(target + 1 ,0)); 
        // 每次石头有两种可能，加入 或者 不加入
        for(int i = 1; i <= n; i ++) {
            for(int j = 1; j <= target; j ++) {
                if(j - stones[i - 1] >= 0) // 加入的话要确保背包的容量够大
                    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - stones[i - 1]] + stones[i - 1] );
                else dp[i][j] = dp[i - 1][j];
            }
        }
        return (sum - 2 * dp[n][target]);
    }
};

class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        int n = stones.size();
        int sum = 0;
        for(int t : stones) sum += t;
        int target = sum / 2; // 背包容量：target 求放进去的物品的最大重量MaxWeight
        // dp[i][j]含义:从前i块石头中选取，选取值之和小于等于目标值j的最大值
        vector<int> dp(target + 1 ,0); 
        // 每次石头有两种可能，加入 或者 不加入
        for(int e: stones) {
            for(int j = target; j >= e; j --) {
                dp[j] = max(dp[j], dp[j - e] + e);
            }
        }
        return (sum - 2 * dp[target]);
    }
};

494. 目标和

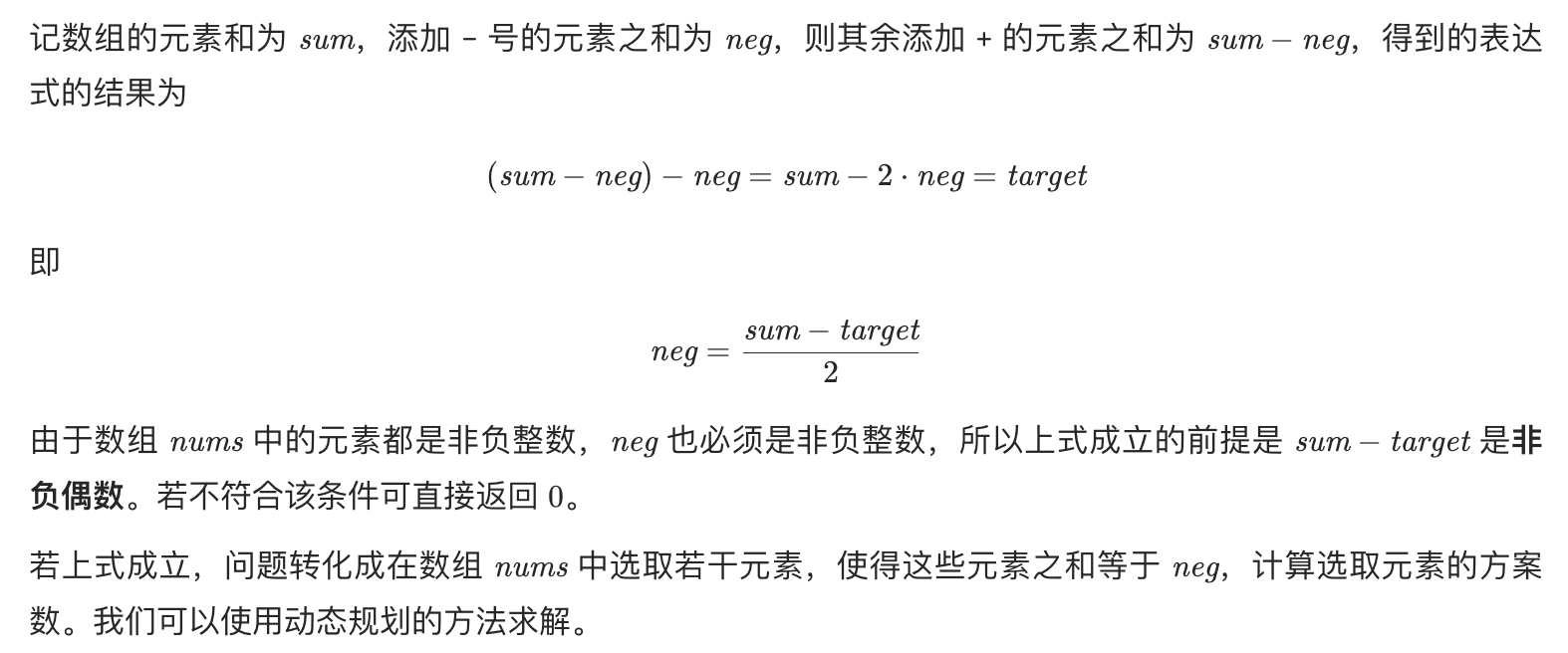
给你一个整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

• 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1：

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

输入：nums = [1], target = 1
输出：1

提示：

• 1 <= nums.length <= 20
• 0 <= nums[i] <= 1000
• 0 <= sum(nums[i]) <= 1000
• -1000 <= target <= 1000

C++

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for (int i = 0; i < nums.size(); i++) sum += nums[i];
        if ((target + sum) % 2 == 1) return 0; // 此时没有方案
        if(target + sum < 0) return 0;
        int bagSize = (target + sum) / 2;

        vector<int> dp(bagSize + 1,0);// dp[bagSize]：让背包容量恰好为bagSize的方法数
        dp[0] = 1;
        for(int e: nums) {
            for(int j = bagSize; j >= e; j --) {
                dp[j] += dp[j - e];  
            }
        }
        return dp[bagSize];
    }
};

474. 一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {"0", "1"} ，所以答案是 2 。

提示：

• 1 <= strs.length <= 600
• 1 <= strs[i].length <= 100
• strs[i] 仅由 '0' 和 '1' 组成
• 1 <= m, n <= 100

C++

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        // dp[m][n] 代表1总量不超过m,0数量不超过n的最大子集数 相当于容量有两个维度的一维数组
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0)); 
        for(string s: strs){
            int oneNum = 0, zeroNum = 0;
            for (char c : s) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
};