DP之子序列合集

300. 最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

C++

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n, 1);
        if(n == 1) return 1;
        for(int i = 1; i < n; i ++) {
            for(int j = 0; j < i; j ++) {
                if(nums[j] < nums[i]) dp[i] = max(dp[i], dp[j] + 1); 
            }
        }
        return *max_element(dp.begin(), dp.end());
    }
};

674. 最长连续递增序列

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。 

示例 2：

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

提示：

• 1 <= nums.length <= 104
• -109 <= nums[i] <= 109

C++

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n + 1, 1);
        dp[0] = 0;
        for(int i = 2; i <= n; i ++) {
            if( nums[i - 1] > nums[i  - 2]) dp[i] = dp[i - 1] + 1;
        }
        return *max_element(dp.begin(), dp.end());
    }
};

718. 最长重复子数组

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

示例 1：

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

提示：

• 1 <= nums1.length, nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 100

C++

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        // 以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]
        int m = nums1.size();
        int n = nums2.size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        int res = 0;
        for(int i = 1; i <= m ; i ++) {
            for(int j = 1; j <= n; j ++) {
                if(nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i-1][j-1] + 1;
                    res = max(res, dp[i][j]);
                }
            }
        }
        return res;
    }
};

1143. 最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

示例 3：

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

提示：

• 1 <= text1.length, text2.length <= 1000
• text1 和 text2 仅由小写英文字符组成。

C++

/*
如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

不用返回dp数组里的最大元素.因为dp[i][j]表示子数组一定取到i-1，j-1的元素， dp[i][j]表示子序列不一定取到

*/
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m = text1.size();
        int n = text2.size();
        // text1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;
        // 同理dp[0][j]也是0
        // 其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。
        vector<vector<int>> dp(m +1, vector<int>(n + 1, 0));
        for(int i = 1; i<= m; i++) {
            for(int j =1; j <=n; j ++) {
                if(text1[i - 1] == text2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                dp[i][j] = max({dp[i][j- 1], dp[i - 1][j], dp[i][j]});
            }
        }
        return dp[m][n];
    }
};

1035. 不相交的线

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

• nums1[i] == nums2[j]
• 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

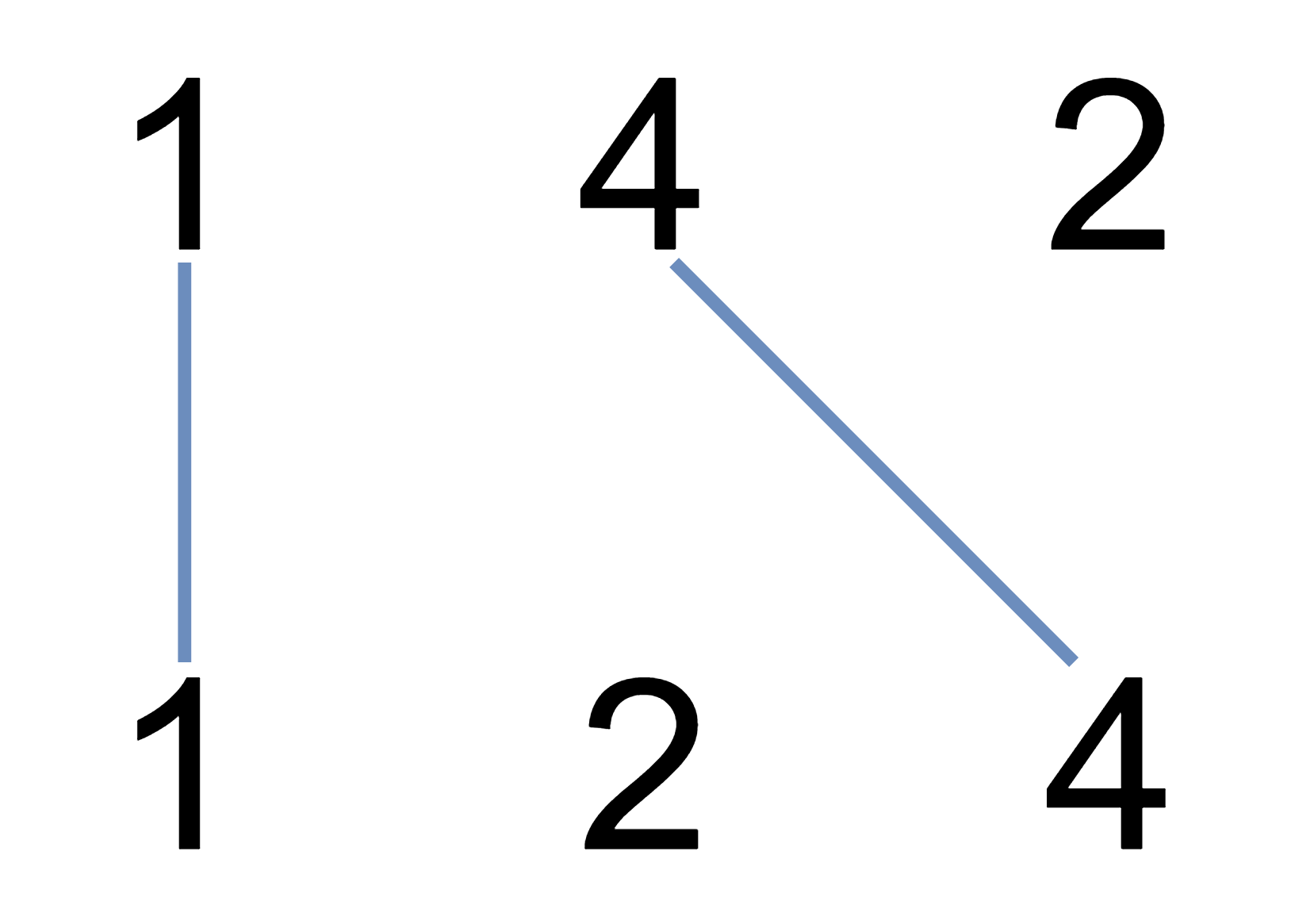
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

提示：

• 1 <= nums1.length, nums2.length <= 500
• 1 <= nums1[i], nums2[j] <= 2000

C++

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size();
        int n = nums2.size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        for(int i = 1; i <= m; i ++) {
            for(int j = 1; j <= n; j ++) {
                if(nums1[i - 1] == nums2[j - 1]){
                    dp[i][j] = dp[i -1][j - 1] + 1;
                }
                dp[i][j] = max({dp[i][j - 1], dp[i - 1][j], dp[i][j]});
            }
        }
        return dp[m][n];
    }
};

53. 最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

C++

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n+1, -1e8);
        for(int i = 1; i <=n; i ++){
            dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);
        }
        return *max_element(dp.begin(), dp.end());
    }
};

392. 判断子序列

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

C++

• 思路1: 同 1143.最长公共子序列

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int m = s.size();
        int n = t.size();
        if(n < m) return false;
        if(m == 0) return true;

        // dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。
        vector<vector<int>> dp(n +1 , vector<int>(m + 1, 0));  
        for(int i = 1; i <=n ; i ++){
            for(int j = 1; j <= m; j ++) {
                if(t[i - 1] == s[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max({dp[i - 1][j],dp[i][j- 1], dp[i][j]});
            }  
        }
        return dp[n][m] == m;
    }
};

• 思路2:

else dp[i][j] = max({dp[i - 1][j],dp[i][j- 1], dp[i][j]});
//换成 else dp[i][j] = dp[i - 1][j]; 表示跳过 t的这一项，等于前面一项

583. 两个字符串的删除操作

给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。

每步 可以删除任意一个字符串中的一个字符。

示例 1：

输入: word1 = "sea", word2 = "eat"
输出: 2
解释: 第一步将 "sea" 变为 "ea" ，第二步将 "eat "变为 "ea"

示例 2:

输入：word1 = "leetcode", word2 = "etco"
输出：4

提示：

• 1 <= word1.length, word2.length <= 500
• word1 和 word2 只包含小写英文字母

C++

• 思路，找出最长公共子序列， 操作数即为两个字符串的长度之和 - 两倍的最长公共子序列长度

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size();
        int n = word2.size();
        vector<vector<int>> dp (m+1, vector<int>(n +1, 0));
        for(int i = 1; i <= m; i ++) {
            for(int j = 1; j <= n; j ++) {
                if( word1[i - 1] == word2[ j - 1]) 
                    dp[i][j] = 1 +dp[i - 1][j - 1];
                else dp[i][j] = max({dp[i][j - 1], dp[i - 1][j], dp[i][j]});
            }
        } 
        return (m + n - 2 * dp[m][n]);
    }
};