贪心算法之提高题合集

134. 加油站

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则保证它是唯一的。

示例 1:

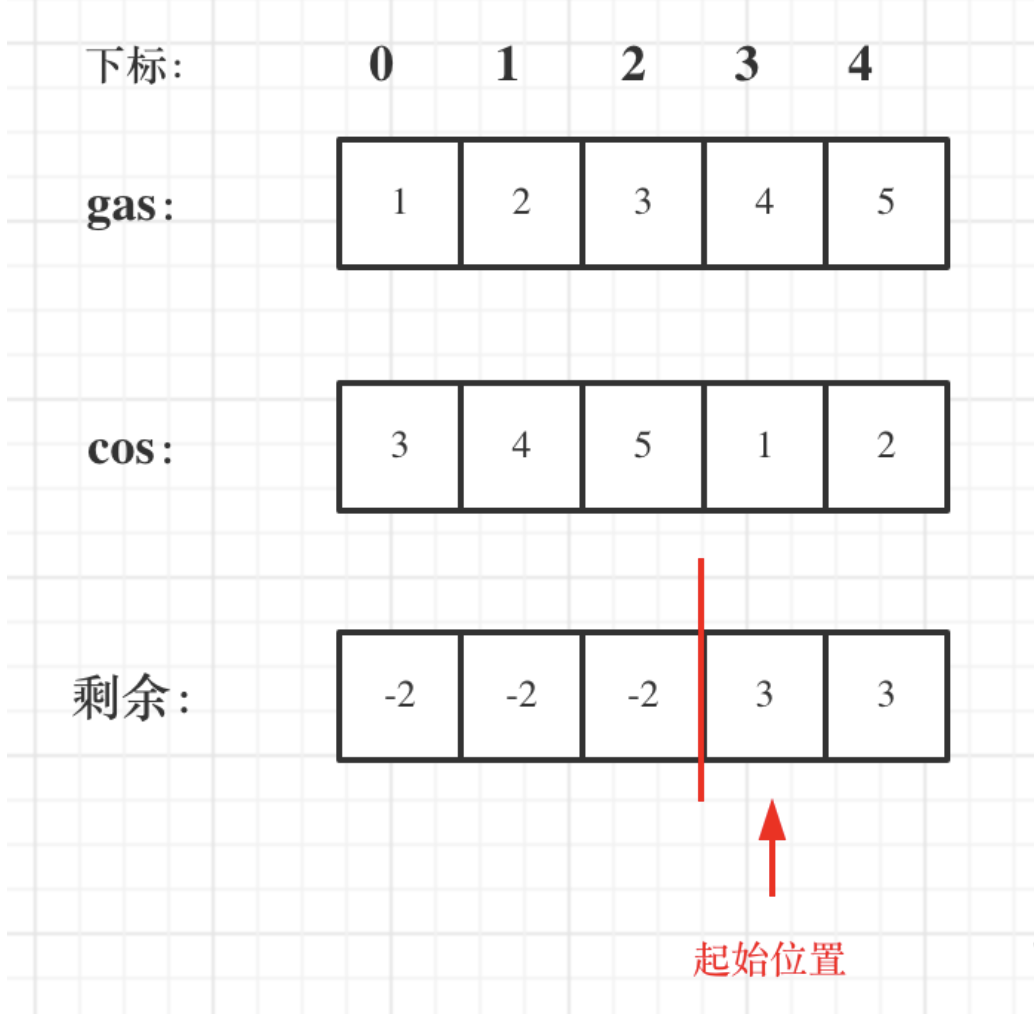
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

提示:

gas.length == n
cost.length == n
1 <= n <= 105
0 <= gas[i], cost[i] <= 104

C++

/*
i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，起始位置从i+1算起，再从0计算curSum。
*/
class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int n = gas.size();
        vector<int> rest(n,0);
        int sum = 0;
        for(int i = 0; i < n; i ++){
            rest[i] = gas[i] - cost[i];
            sum += rest[i];
        }
        if(sum < 0) return -1; // 一定跑不完一圈

        int curSum = 0;
        int res = 0;
        for(int i =0; i < n; i ++) {
            curSum += rest[i];
            if(curSum < 0) {
                curSum = 0;
                res = i + 1;
            }
        }
        return res;
    }
};

968. 监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。计算监控树的所有节点所需的最小摄像头数量。

示例 1：

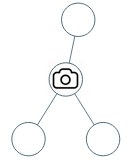
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

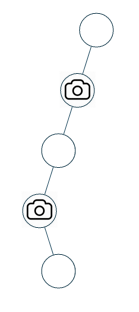
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 0：该节点安装了监视器 1：该节点可观，但没有安装监视器 2：该节点不可观
class Solution {
public:
    int res = 0;
    int minCameraCover(TreeNode* root) {
        if(!root) return 0;
        if(dfs(root) == 2) res ++; // root不可观， 要在root上装一个
        return res;
    }
    int dfs(TreeNode* root) {
        if(root == nullptr) return 1;
        int left = dfs(root -> left);
        int right = dfs(root -> right);
        if(left == 2 || right == 2){
            res ++;
            return 0; // 这点装了监视器
        }else if(left == 0 || right == 0) {
            return 1;
        }else return 2;
    }
};