力扣HOT100部分合集

75. 颜色分类

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，**原地**对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题。

示例 ：

输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]

提示：

• n == nums.length
• 1 <= n <= 300
• nums[i] 为 0、1 或 2

C++

class Solution {
public:
    void sortColors(vector<int>& nums) {
        int n = nums.size();
        if(n < 2) return;

        int zero = 0, two = n;
        int i = 0;
        while(i < two){
            if(nums[i] == 0){
                swap(nums[i], nums[zero]);
                i ++;
                zero ++;
            }else if(nums[i] == 1){
                i ++;
            }else{
                two --;
                swap(nums[i], nums[two]);
            }
        }
        return;
    }
};

105. 从前序与中序遍历序列构造二叉树

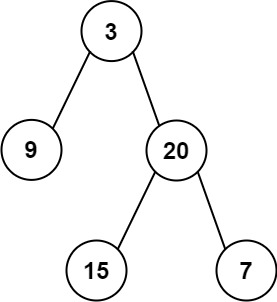
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return dfs(preorder, inorder, 0, inorder.size() - 1);
    }

    TreeNode* dfs(vector<int>& preorder, vector<int>& inorder, int l, int r){ // [左，右]
        if(l < 0 || r >= inorder.size() || l > r || preorder.size() == 0) return nullptr;
        int num = preorder.front();
        preorder.erase(preorder.begin());
        TreeNode* t = new TreeNode(num);
        for(int i = l; i <= r; i ++){
            if(inorder[i] == num){
                t -> left = dfs(preorder, inorder, l, i - 1);
                t -> right = dfs(preorder, inorder, i + 1, r);
            }
        }
        return t;
    }
};

128. 最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1：

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

示例 2：

输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

提示：

• 0 <= nums.length <= 105
• -109 <= nums[i] <= 109

C++

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> st;
        for(auto e: nums)
            st.insert(e);
        
        int res = 0;
        for(auto e : st){
            if(!st.count(e - 1)){
                int curNum = e;
                int longStreak = 1;

                while(st.count(curNum + 1)){
                    longStreak += 1;
                    curNum += 1;
                }
                res = max(res, longStreak);
            }
        }
        return res;
    }
};

208. 实现 Trie (前缀树)

**Trie**（发音类似 “try”）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

• Trie() 初始化前缀树对象。
• void insert(String word) 向前缀树中插入字符串 word 。
• boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
• boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // 返回 True
trie.search("app");     // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app");     // 返回 True

提示：

• 1 <= word.length, prefix.length <= 2000
• word 和 prefix 仅由小写英文字母组成
• insert、search 和 startsWith 调用次数 总计 不超过 3 * 104 次

C++

class Trie {
private:
    vector<Trie*> children;
    bool isEnd;

    Trie* searchPrefix(string prefix){ // 如果存在的话，返回prefix的最后一个字符所在树节点
        Trie* node = this;
        for(auto ch: prefix){
            int num = ch -'a';
            if(node -> children[num] == nullptr) return nullptr;
            else node = node -> children[num];
        }
        return node;
    }
public:
    Trie() :children(26), isEnd(false){}
    
    void insert(string word) {
        Trie* node = this;
        for(auto ch : word){
            int num = ch -'a';
            if(node -> children[num] == nullptr){
                node -> children[num] = new Trie();
            }
            node = node -> children[num];
        }
        node -> isEnd = true;
    }
    
    bool search(string word) {
        Trie* res = searchPrefix(word);
        if(res) return res -> isEnd;
        return false;
    }
    
    bool startsWith(string prefix) {
        Trie* res = searchPrefix(prefix);
        if(res) return true;
        return false;
    }
};

253. 会议室 II

给你一个会议时间安排的数组 intervals ，每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ，返回 所需会议室的最小数量 。

示例 1：

输入：intervals = [[0,30],[5,10],[15,20]]
输出：2

示例 2：

输入：intervals = [[7,10],[2,4]]
输出：1

提示：

• 1 <= intervals.length <= 104
• 0 <= starti < endi <= 106

C++

class Solution {
public:
    int minMeetingRooms(vector<vector<int>>& intervals) {
        int n = intervals.size();
        if(n <= 1) return n;
        sort(intervals.begin(),intervals.end());
        vector<vector<int>> res;
        for(auto e: intervals){
            if(res.size() == 0) {
                res.push_back(e);
                continue;
            }
            for(int i = 0; i < res.size(); i++){
                if(e[0] >= res[i][1]) {
                    res[i] = e;
                    break;
                }
                if(i == res.size() - 1) {
                    res.push_back(e);
                    break;
                }
            }
        }
        return res.size();
    }
};

287. 寻找重复数

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

示例 1：

输入：nums = [1,3,4,2,2]
输出：2

示例 2：

输入：nums = [3,1,3,4,2]
输出：3

提示：

• 1 <= n <= 105
• nums.length == n + 1
• 1 <= nums[i] <= n
• nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次

C++

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int n = nums.size();
        int l = 0, r = n - 1;
        while (l < r) {
            int mid = (l + r) / 2; 
            int cnt = 0; 
            for(int i = 0; i < n; i ++) // 找nums中有多少数 <= mid
                cnt += nums[i] <= mid; 
            if(cnt <= mid) l = mid + 1;  
            else r = mid; 
        }
        return l;
    }
};

347. 前 K 个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

输入: nums = [1], k = 1
输出: [1]

提示：

• 1 <= nums.length <= 105
• k 的取值范围是 [1, 数组中不相同的元素的个数]
• 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

C++

• 优先队列

class Solution {
public:

    // 小顶堆
    class mycomparison {
    public:
        bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
            return lhs.second > rhs.second;
        }
    };

    vector<int> topKFrequent(vector<int>& nums, int k) {
        map<int, int> mp;
        for(int e: nums)
            mp[e]++;

        priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que; // priority_queue<Type, Container, Functional> 

        for(auto i = mp.begin(); i != mp.end(); i ++){
            pri_que.push(*i);
            if(pri_que.size() > k)  pri_que.pop();// 如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
        }

        // 找出前K个高频元素，因为小顶堆先弹出的是最小的，所以倒叙来输出到数组
        vector<int> res(k);
        for (int i = k - 1; i >= 0; i--) {
            res[i] = pri_que.top().first;
            pri_que.pop();
        }
        return res;
    }
};

394. 字符串解码

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

示例 1：

输入：s = "3[a2[c]]"
输出："accaccacc"

示例 2：

输入：s = "2[abc]3[cd]ef"
输出："abcabccdcdcdef"

提示：

• 1 <= s.length <= 30
• s 由小写英文字母、数字和方括号 '[]' 组成
• s 保证是一个 有效 的输入。
• s 中所有整数的取值范围为 [1, 300]

C++

• 递归

/*
当 s[i] == ']' 时，返回当前括号内记录的 res 字符串与 ] 的索引 i （更新上层递归指针位置）；
当 s[i] == '[' 时，开启新一层递归，记录此 [...] 内字符串 tmp 和递归后的最新索引 i，并执行 res + multi * tmp 拼接字符串。
遍历完毕后返回 res。
*/
class Solution {
public:
    string src; 
    unsigned int ptr; // unsigned int
     
    string decodeString(string s) {
        src = s;
        ptr = 0;
        return getString();
    }
    
    int getDigits() { // 停在数字后第一个非数字处
        int ret = 0;
        while (ptr < src.size() && isdigit(src[ptr])) 
            ret = ret * 10 + src[ptr++] - '0';
        return ret;
    }

    string getString() {
        if (ptr == src.size() || src[ptr] == ']')  return "";

        string ret;
        if (isdigit(src[ptr])) {
            int k = getDigits(); 
            ++ ptr; // 过滤左括号
            string str = getString(); 
            ++ ptr; // 过滤右括号
            while (k --) ret += str; // 构造字符串
        } 
        else if (isalpha(src[ptr]))
            ret = string(1, src[ptr++]);
        
        return ret + getString();
    }

};

560. 和为 K 的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的连续子数组的个数 。

示例 1：

输入：nums = [1,1,1], k = 2
输出：2

提示：

• 1 <= nums.length <= 2 * 104
• -1000 <= nums[i] <= 1000
• -107 <= k <= 107

C++

• 前缀和

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int sum = 0, res = 0;
        unordered_map<int, int> mp; // <前缀和，对应的前缀和的个数>
        mp[0] = 1;
        for (auto e : nums) {
            sum += e; 
            res += mp[sum - k]; 
            mp[sum] ++;
        }
        return res;
    }
};

438. 找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

示例 1:

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

示例 2:

输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。

提示:

• 1 <= s.length, p.length <= 3 * 104
• s 和 p 仅包含小写字母

C++

class Solution {
public:
    // 滑动窗口
    vector<int> findAnagrams(string s, string p) {
        int sLen = s.size(), pLen = p.size();
        if (sLen < pLen) return {};

        vector<int> res;
        vector<int> sCount(26);
        vector<int> pCount(26);

        for (int i = 0; i < pLen; ++i) {
            sCount[s[i] - 'a'] ++;
            pCount[p[i] - 'a'] ++;
        }
        if (sCount == pCount) res.emplace_back(0);

        for(int i = 0; i + pLen < sLen; i ++){
            sCount[s[i] - 'a'] --;
            sCount[s[i + pLen] - 'a'] ++;
            if(sCount == pCount) res.push_back(i + 1);
        }

        return res;

    }
};

621. 任务调度器

给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行，并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间，CPU 可以完成一个任务，或者处于待命状态。

然而，两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间，因此至少有连续 n 个单位时间内 CPU 在执行不同的任务，或者在待命状态。

你需要计算完成所有任务所需要的 最短时间 。

示例 1：

输入：tasks = ["A","A","A","B","B","B"], n = 2
输出：8
解释：A -> B -> (待命) -> A -> B -> (待命) -> A -> B
     在本示例中，两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间，而执行一个任务只需要一个单位时间，所以中间出现了（待命）状态。 

示例 2：

输入：tasks = ["A","A","A","B","B","B"], n = 0
输出：6
解释：在这种情况下，任何大小为 6 的排列都可以满足要求，因为 n = 0
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
诸如此类

示例 3：

输入：tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
输出：16
解释：一种可能的解决方案是：
     A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> (待命) -> (待命) -> A -> (待命) -> (待命) -> A

提示：

• 1 <= task.length <= 104
• tasks[i] 是大写英文字母
• n 的取值范围为 [0, 100]

C++

• https://leetcode.cn/problems/task-scheduler/solution/tong-zi-by-popopop/

class Solution {
public:
    int leastInterval(vector<char>& tasks, int n) {
        int len = tasks.size();
        vector<int> vec(26); // 统计每种任务的数量
        for(auto e : tasks) vec[e - 'A'] ++;
        sort(vec.rbegin(),vec.rend()); // vec[0]为最多的任务数
        int cnt = 1; // 需要记录有多个任务数量都最大且相同, 用于标记最后一个桶的任务数。
        while(cnt < vec.size() && vec[cnt] == vec[0]) cnt++;
        return max(len, cnt+(n+1)*(vec[0]-1));
    }
};