给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = , nums2 = 输出:2.00000 解释:合并数组 = ,中位数 2
示例 2:
输入:nums1 = [1 ,2 ], nums2 = [3 ,4 ] 输出:2.50000 解释:合并数组 = [1 ,2 ,3 ,4 ] ,中位数 / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
C++
二分 : O(lg(m + n))
合并 O(m + n)
class Solution {public : double findMedianSortedArrays (vector<int >& nums1, vector<int >& nums2) vector<int > res = merge (nums1, nums2, 0 , 0 ); int a = nums1.size (), b = nums2.size (); int idx1 = (a + b)/2 ; int idx2 = (a + b) % 2 ? idx1 : idx1 - 1 ; return (double )(res[idx1] + res[idx2])/2 ; } vector<int > merge (vector<int > a, vector<int > b, int l, int r) { vector<int > s; int i = 0 , j = 0 ; while (i < a.size () && j < b.size ()) { if (a[i] < b[j]) s.push_back (a[i++]); else s.push_back (b[j++]); } while (i < a.size ()) s.push_back (a[i++]); while (j < b.size ()) s.push_back (b[j++]); return s; } };
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
读入字符串并丢弃无用的前导空格
检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数(即,”123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。
如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −231 的整数应该被固定为 −231 ,大于 231 − 1 的整数应该被固定为 231 − 1 。
返回整数作为最终结果。
注意:
本题中的空白字符只包括空格字符 ' ' 。
除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
示例 1:
输入:s = " -42 " 输出:-42 解释: 第 1 步:" -42 "(读入前导空格,但忽视掉) ^ 第 2 步:" -42 "(读入 '-' 字符,所以结果应该是负数) ^ 第 3 步:" -42 "(读入 "42") ^ 解析得到整数 -42 。 由于 "-42 " 在范围 [-231 , 231 - 1] 内,最终结果为 -42 。
示例 2:
输入:s = "4193 with words" 输出:4193 解释: 第 1 步:"4193 with words" (当前没有读入字符,因为没有前导空格) ^ 第 2 步:"4193 with words" (当前没有读入字符,因为这里不存在 '-' 或者 '+' ) ^ 第 3 步:"4193 with words" (读入 "4193" ;由于下一个字符不是一个数字,所以读入停止) ^ 解析得到整数 4193 。 由于 "4193" 在范围 [-231 , 231 - 1 ] 内,最终结果为 4193 。
提示:
0 <= s.length <= 200s 由英文字母(大写和小写)、数字(0-9)、' '、'+'、'-' 和 '.' 组成
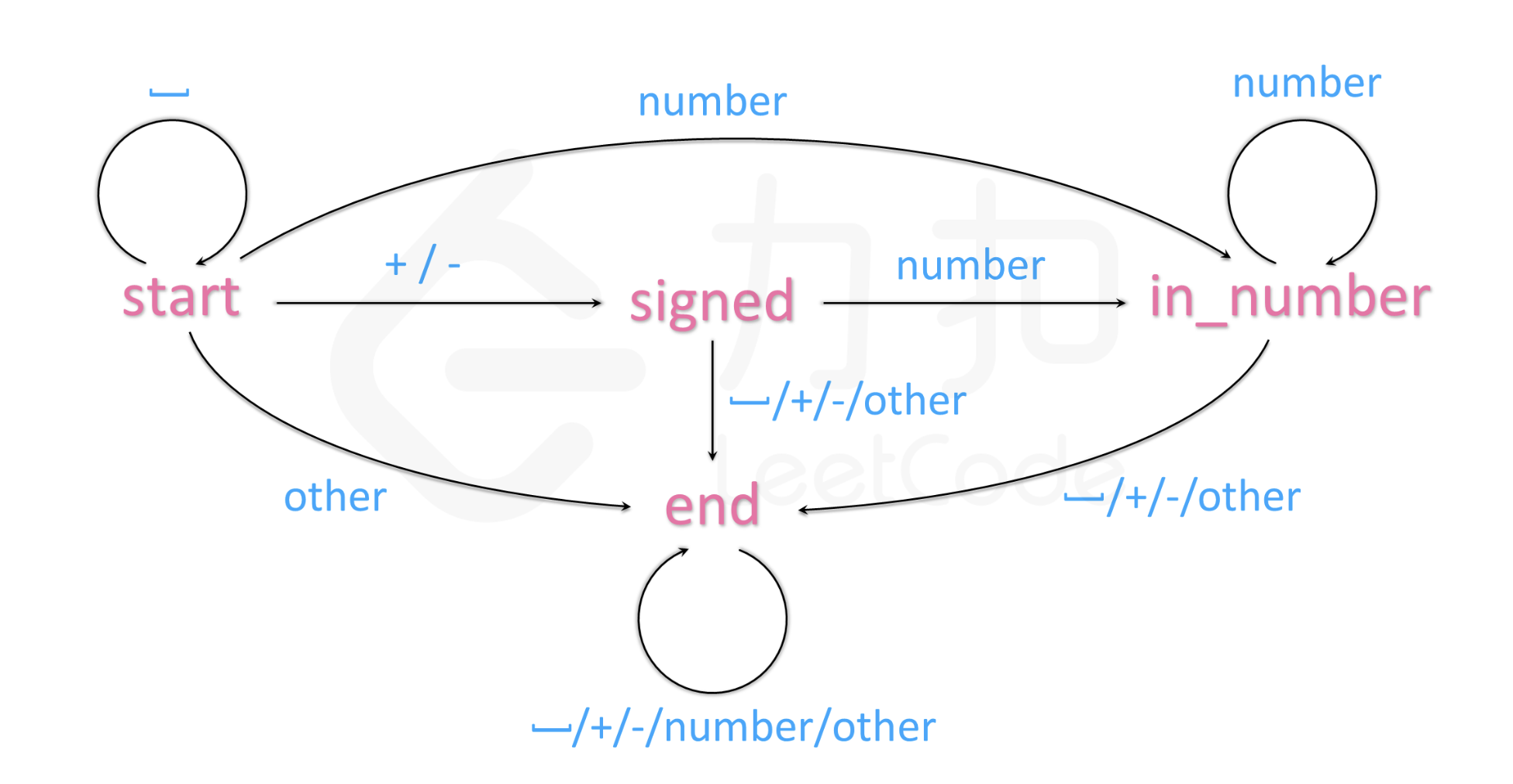
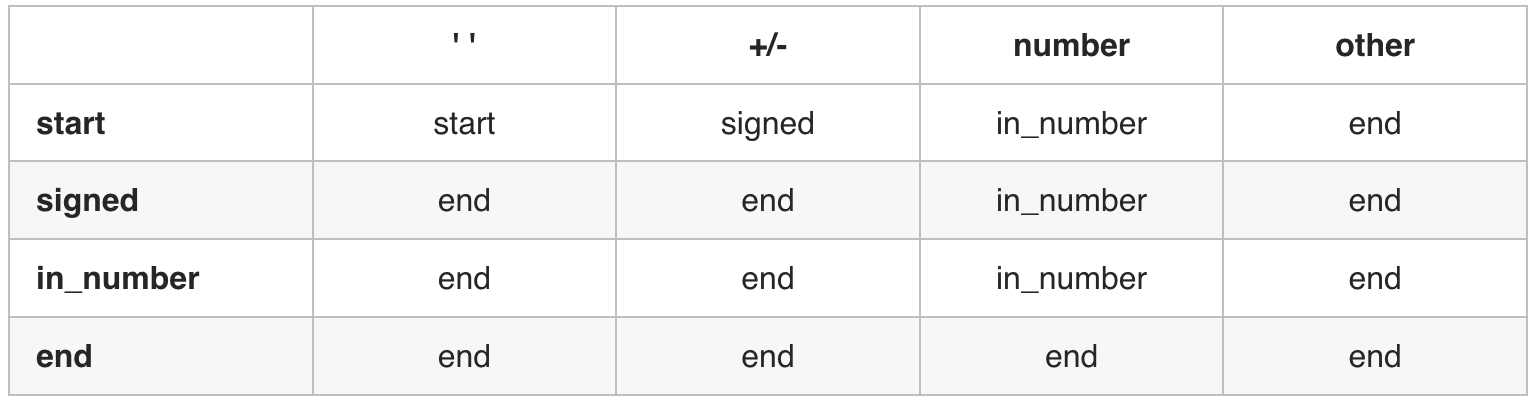
C++ class Automaton { string state = "start" ; map<string, vector<string>> mp{ {"start" ,{"start" , "signed" , "in_number" , "end" }}, {"signed" ,{"end" , "end" , "in_number" , "end" }}, {"in_number" ,{"end" , "end" , "in_number" , "end" }}, {"end" ,{"end" , "end" , "end" , "end" }} }; int getCol (char ch) if (isspace (ch)) return 0 ; if (ch == '-' || ch == '+' ) return 1 ; if (isdigit (ch)) return 2 ; else return 3 ; } public : long long res = 0 ; int sign = 1 ; void get (char ch) state = mp[state][getCol (ch)]; if (state == "in_number" ) { res = res * 10 + ch - '0' ; res = sign == 1 ? min (res, (long long )INT_MAX) : min (res, -(long long )INT_MIN); } else if (state == "signed" ) sign = ch == '+' ? 1 : -1 ; else if (state == "end" ) return ; } }; class Solution {public : int myAtoi (string s) Automaton automaton; for (char ch : s) automaton.get (ch); return automaton.sign * automaton.res; } };
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa" , p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa" , p = "a*" 输出:true 解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a' 。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab" , p = ".*" 输出:true 解释:".*" 表示可匹配零个或多个('*' )任意字符('.' )。
提示:
1 <= s.length <= 201 <= p.length <= 30s 只包含从 a-z 的小写字母。p 只包含从 a-z 的小写字母,以及字符 . 和 *。保证每次出现字符 * 时,前面都匹配到有效的字符
C++ class Solution {public : bool isMatch (string s, string p) int m = s.size (), n = p.size (); auto matches = [&](int i, int j) { if (i == 0 || j == 0 ) return false ; if (p[j - 1 ] == '.' ) return true ; return s[i - 1 ] == p[j - 1 ]; }; vector<vector<bool >> dp (m + 1 , vector <bool >(n + 1 )); dp[0 ][0 ] = true ; for (int i = 0 ; i <= m; i ++){ for (int j = 1 ; j <= n; j++){ if (islower (p[j - 1 ]) || p[j - 1 ] == '.' ){ if (matches (i, j)) dp[i][j] = dp[i - 1 ][j - 1 ]; } else { if (matches (i, j - 1 )) dp[i][j] = dp[i - 1 ][j] || dp[i][j - 2 ]; else dp[i][j] = dp[i][j - 2 ]; } } } return dp[m][n]; } };
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC" , t = "ABC" 输出:"BANC" 解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
示例 2:
输入:s = "a" , t = "a" 输出:"a" 解释:整个字符串 s 是最小覆盖子串。
示例 3:
输入: s = "a" , t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中, 因此没有符合条件的子字符串,返回空字符串。
提示:
m == s.lengthn == t.length1 <= m, n <= 105s 和 t 由英文字母组成
进阶: 你能设计一个在 o(m+n) 时间内解决此问题的算法吗?
C++ class Solution {public : string minWindow (string s, string t) { map<char , int > ms, mt; for (auto e: t) mt[e] ++; string res; int cnt = 0 ; for (int r = 0 , l = 0 ; r < s.size (); r ++ ) { ms[s[r]] ++ ; if (ms[s[r]] <= mt[s[r]]) cnt ++ ; while (ms[s[l]] > mt[s[l]]) ms[s[l ++ ]] -- ; if (cnt == t.size ()) { if (res.empty () || r - l + 1 < res.size ()) res = s.substr (l, r - l + 1 ); } } return res; } };
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
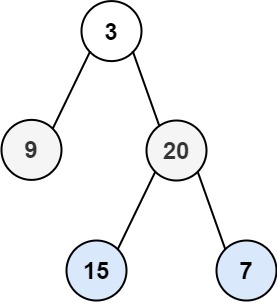
示例 :
提示:
树中节点数目在范围 [0, 2000] 内
-100 <= Node.val <= 100
C++ class Solution {public : vector<vector<int >> zigzagLevelOrder (TreeNode* root) { if (!root) return {}; bool isLeftToRight = false ; queue<TreeNode*> q; q.push (root); vector<vector<int >> res; while (!q.empty ()){ int n = q.size (); deque<int > levelList; while (n -- > 0 ){ TreeNode* t = q.front (); q.pop (); isLeftToRight ? levelList.push_back (t -> val) : levelList.push_front (t -> val); if (t -> left) q.push (t -> left); if (t -> right) q.push (t -> right); } } isLeftToRight = !isLeftToRight; res.emplace_back (vector<int >{levelList.begin (), levelList.end ()}); } return res; } };
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
有效的算符为 '+'、'-'、'*' 和 '/' 。
每个操作数(运算对象)都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2" ,"1" ,"+" ,"3" ,"*" ] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1 ) * 3 ) = 9
示例 2:
输入:tokens = ["10" ,"6" ,"9" ,"3" ,"+" ,"-11" ,"*" ,"/" ,"*" ,"17" ,"+" ,"5" ,"+" ] 输出:22 解释:该算式转化为常见的中缀算术表达式为: ((10 * (6 / ((9 + 3 ) * -11 ))) + 17 ) + 5 = ((10 * (6 / (12 * -11 ))) + 17 ) + 5 = ((10 * (6 / -132 )) + 17 ) + 5 = ((10 * 0 ) + 17 ) + 5 = (0 + 17 ) + 5 = 17 + 5 = 22
提示:
1 <= tokens.length <= 104tokens[i] 是一个算符("+"、"-"、"*" 或 "/"),或是在范围 [-200, 200] 内的一个整数
C++ class Solution {public : int evalRPN (vector<string>& tokens) if (tokens.size () == 1 ) return stoi (tokens[0 ]); stack<int > stkNum; stack<string> stkOperator; int i = 0 ; while (i < tokens.size ()){ while (stkOperator.empty ()){ if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/" ) stkOperator.emplace (tokens[i++]); else stkNum.emplace (stoi (tokens[i++])); } auto op = stkOperator.top (); stkOperator.pop (); auto b = stkNum.top (); stkNum.pop (); auto a = stkNum.top (); stkNum.pop (); auto c = 0 ; if (op == "+" ) c = a + b; if (op == "-" ) c = a - b; if (op == "*" ) c = a * b; if (op == "/" ) c = a / b; stkNum.emplace (c); } return stkNum.top (); } };
给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。
注意: 输出结果可能非常大,所以你需要返回一个字符串而不是整数。
示例 1:
示例 2:
输入:nums = [3,30,34,5 ,9 ] 输出:"9534330 "
提示:
1 <= nums.length <= 1000 <= nums[i] <= 109
C++ class Solution {public : static bool cmp (const int a, const int b) string sa = to_string (a), sb = to_string (b); return sa + sb > sb + sa; } string largestNumber (vector<int >& nums) { string res; sort (nums.begin (), nums.end (), cmp); for (auto e: nums){ res += to_string (e); } if (res[0 ] == '0' ) res.resize (1 ); return res; } };
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入 : nums = [1,2,3,4,5,6,7], k = 3 输出 : [5,6,7,1,2,3,4] 解释 : 向右轮转 1 步 : [7,1,2,3,4,5,6] 向右轮转 2 步 : [6,7,1,2,3,4,5] 向右轮转 3 步 : [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1 ,-100 ,3,99], k = 2 输出:[3,99,-1 ,-100 ] 解释: 向右轮转 1 步: [99,-1 ,-100 ,3] 向右轮转 2 步: [3,99,-1 ,-100 ]
提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 10 <= k <= 105
进阶:
尽可能想出更多的解决方案,至少有 三种 不同的方法可以解决这个问题。
你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗?
C++ class Solution {public : void rotate (vector<int >& nums, int k) vector<int > temp (nums.size()) ; for (int i = 0 ; i < nums.size (); i ++){ temp[(i + k) % nums.size ()] = nums[i]; } nums.assign (temp.begin (), temp.end ()); return ; } };
给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。
示例 1:
输入:n = 10 输出:4 解释:小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
示例 2:
示例 3:
提示:
C++ class Solution {public : int countPrimes (int n) vector<int > isPrime (n, 1 ) ; int res = 0 ; for (int i = 2 ; i < n; ++i) { if (isPrime[i]) { res += 1 ; if ((long long )i * i < n) { for (int j = i * i; j < n; j += i) { isPrime[j] = 0 ; } } } } return res; } };
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。
注意: 不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
示例 1:
示例 2:
提示:
1 <= s.length <= 3 * 105s 由整数和算符 ('+', '-', '*', '/') 组成,中间由一些空格隔开s 表示一个 有效表达式 表达式中的所有整数都是非负整数,且在范围 [0, 231 - 1] 内
题目数据保证答案是一个 32-bit 整数
C++ class Solution {public : int calculate (string s) vector<int > stk; char preSign = '+' ; int num = 0 ; int n = s.length (); for (int i = 0 ; i < n; ++i) { if (isdigit (s[i])) num = num * 10 + int (s[i] - '0' ); if ((!isdigit (s[i]) && !isspace (s[i])) || i == n - 1 ) { switch (preSign) { case '+' : stk.push_back (num); break ; case '-' : stk.push_back (-num); break ; case '*' : stk.back () *= num; break ; default : stk.back () /= num; } preSign = s[i]; num = 0 ; } } return accumulate (stk.begin (), stk.end (), 0 ); } };
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1 ,-3 ,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1 ] -3 5 3 6 7 3 1 [3 -1 -3 ] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
示例 2:
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
C++
multiset 可重复set,内部用红黑树实现,可排序 begin()最小, rbegin()最大
class Solution {public : vector<int > maxSlidingWindow (vector<int >& nums, int k) { if (k == 1 ) return nums; multiset<int > pq; vector<int > res; int l = 0 ; int r = l + k - 1 ; for (int i = l; i <= r; i ++) pq.insert (nums[i]); res.push_back (*pq.rbegin ()); while (r < nums.size () - 1 ){ pq.insert (nums[++r]); auto it = pq.find (nums[l++]); pq.erase (it); res.push_back (*pq.rbegin ()); } return res; } };
class Solution {public : vector<int > maxSlidingWindow (vector<int >& nums, int k) { int n = nums.size (); priority_queue<pair<int , int >> q; for (int i = 0 ; i < k; ++i) { q.emplace (nums[i], i); } vector<int > ans = {q.top ().first}; for (int i = k; i < n; ++i) { q.emplace (nums[i], i); while (q.top ().second <= i - k) { q.pop (); } ans.push_back (q.top ().first); } return ans; } };
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
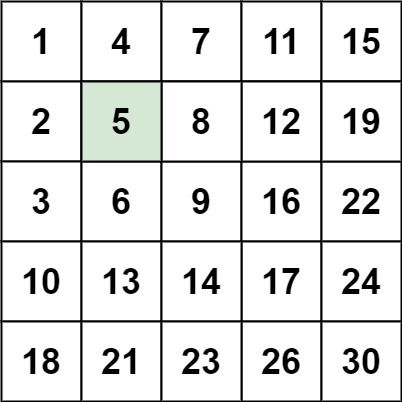
示例 1:
输入:matrix = , target = 5 输出:true
C++ class Solution {public : bool searchMatrix (vector<vector<int >>& matrix, int target) int m = matrix.size (); int n = matrix[0 ].size (); int i = 0 , j = n - 1 ; while (i < m && j >= 0 ){ if (matrix[i][j] == target) return true ; else if (matrix[i][j] < target) i ++; else j --; } return false ; } };
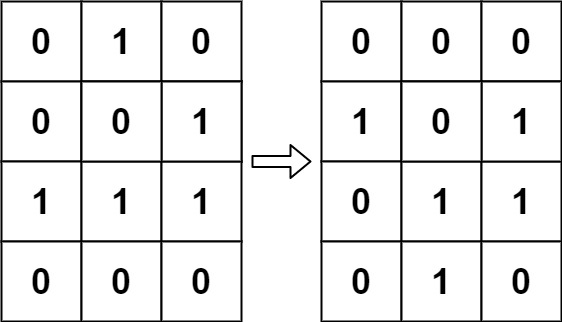
根据 百度百科 , 生命游戏 ,简称为 生命 ,是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态: 1 即为 活细胞 (live),或 0 即为 死细胞 (dead)。每个细胞与其八个相邻位置(水平,垂直,对角线)的细胞都遵循以下四条生存定律:
如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡;
如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活;
如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡;
如果死细胞周围正好有三个活细胞,则该位置死细胞复活;
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的,其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态,返回下一个状态。
示例 :
提示:
m == board.lengthn == board[i].length1 <= m, n <= 25board[i][j] 为 0 或 1
C++
原地算法的话,就用复合状态表示每个位置,再重新遍历赋值
class Solution {public : void gameOfLife (vector<vector<int >>& board) int m = board.size (), n = board[0 ].size (); vector<vector<int >> temp (m, vector <int >(n)); for (int i = 0 ; i < m; i ++){ for (int j = 0 ; j < n; j ++){ temp[i][j] = getState (i, j, board); } } for (int i = 0 ; i < m; i ++){ for (int j = 0 ; j < n; j ++){ switch (temp[i][j]){ case (1 ): board[i][j] = 0 ; break ; case (2 ): board[i][j] = 1 ; break ; case (3 ): board[i][j] = 0 ; break ; case (4 ): board[i][j] = 1 ; break ; default : board[i][j] = board[i][j]; break ; } } } return ; } int getAroundOne (int r, int c, vector<vector<int >>& board) int m = board.size (), n = board[0 ].size (); int res = 0 ; for (int i = -1 ; i <= 1 ; i ++){ for (int j = -1 ; j <= 1 ; j ++){ if (r + i < 0 || r + i >= m || c + j < 0 || c + j >= n) continue ; if (board[r + i][c + j]) res++; } } return res - board[r][c]; } int getState (int r, int c, vector<vector<int >>& board) if (getAroundOne (r, c, board) < 2 && board[r][c] == 1 ) return 1 ; if ((getAroundOne (r, c, board) == 2 || getAroundOne (r, c, board) == 3 ) && (board[r][c] == 1 )) return 2 ; if (getAroundOne (r, c, board) > 3 && board[r][c] == 1 ) return 3 ; if (getAroundOne (r, c, board) == 3 && board[r][c] == 0 ) return 4 ; return 5 ; } };
给你一个嵌套的整数列表 nestedList 。每个元素要么是一个整数,要么是一个列表;该列表的元素也可能是整数或者是其他列表。请你实现一个迭代器将其扁平化,使之能够遍历这个列表中的所有整数。
实现扁平迭代器类 NestedIterator :
NestedIterator(List<NestedInteger> nestedList) 用嵌套列表 nestedList 初始化迭代器。int next() 返回嵌套列表的下一个整数。boolean hasNext() 如果仍然存在待迭代的整数,返回 true ;否则,返回 false 。
你的代码将会用下述伪代码检测:
initialize iterator with nestedList res = [] while iterator .hasNext() append iterator .next () to the end of res return res
如果 res 与预期的扁平化列表匹配,那么你的代码将会被判为正确。
示例 1:
输入:nestedList = [[1,1],2,[1,1]] 输出:[1 ,1 ,2 ,1 ,1 ] 解释:通过重复调用 next 直到 hasNext 返回 false ,next 返回的元素的顺序应该是: [1 ,1 ,2 ,1 ,1 ]。
示例 2:
输入:nestedList = 输出: 解释:通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: 。
提示:
1 <= nestedList.length <= 500嵌套列表中的整数值在范围 [-106, 106] 内
C++ class NestedIterator {private : void dfs (vector<NestedInteger> &nestedList) for (auto e : nestedList){ if (e.isInteger ()) all.push_back (e.getInteger ()); else dfs (e.getList ()); } } public : vector<int > all; vector<int >::iterator itr; NestedIterator (vector<NestedInteger> &nestedList) { dfs (nestedList); itr = all.begin (); } int next () return *(itr++); } bool hasNext () return itr < all.end (); } };
请在 n × n 的棋盘上,实现一个判定井字棋胜负的神器,判断每一次玩家落子后,是否有胜出的玩家。
在这个井字棋游戏中,会有 2 名玩家,他们将轮流在棋盘上放置自己的棋子。
在实现这个判定器的过程中,你可以假设以下这些规则一定成立:
每一步棋都是在棋盘内的,并且只能被放置在一个空的格子里;
一旦游戏中有一名玩家胜出的话,游戏将不能再继续;
一个玩家如果在同一行、同一列或者同一斜对角线上都放置了自己的棋子,那么他便获得胜利。
示例:
给定棋盘边长 n = 3, 玩家 1 的棋子符号是 "X" ,玩家 2 的棋子符号是 "O" 。 TicTacToe toe = new TicTacToe(3); toe.move(0, 0, 1); -> 函数返回 0 (此时,暂时没有玩家赢得这场对决) |X | | | | | | | // 玩家 1 在 (0, 0) 落子。 | | |toe.move(0, 2, 2); -> 函数返回 0 (暂时没有玩家赢得本场比赛) |X | |O | | | | | // 玩家 2 在 (0, 2) 落子。 | | |toe.move(2, 2, 1); -> 函数返回 0 (暂时没有玩家赢得比赛) |X | |O | | | | | // 玩家 1 在 (2, 2) 落子。 | |X |toe.move(1, 1, 2); -> 函数返回 0 (暂没有玩家赢得比赛) |X | |O | | |O | | // 玩家 2 在 (1, 1) 落子。 | |X |toe.move(2, 0, 1); -> 函数返回 0 (暂无玩家赢得比赛) |X | |O | | |O | | // 玩家 1 在 (2, 0) 落子。 X | |X |toe.move(1, 0, 2); -> 函数返回 0 (没有玩家赢得比赛) |X | |O | |O |O | | // 玩家 2 在 (1, 0) 落子. X | |X |toe.move(2, 1, 1); -> 函数返回 1 (此时,玩家 1 赢得了该场比赛) |X | |O | |O |O | | // 玩家 1 在 (2, 1) 落子。 X |X |X |
C++ class TicTacToe {private : vector<vector<int >> grid, Row, Col; int mDiagonal,sDiagonal; public : TicTacToe (int n) { grid.resize (n, vector <int >(n)); Row.resize (n, vector <int >(n)); Col.resize (n, vector <int >(n)); mDiagonal,sDiagonal = 0 ; } int move (int row, int col, int player) int n = grid.size (); Col[row][col] += player == 1 ? 1 : -1 ; Row[col][row] += player == 1 ? 1 : -1 ; if (row == col) mDiagonal += player == 1 ? 1 : -1 ; if (row + col == n - 1 ) sDiagonal += player == 1 ? 1 : -1 ; if (abs (accumulate (Row[col].begin (), Row[col].end (), 0 )) == n || abs (accumulate (Col[row].begin (), Col[row].end (), 0 )) == n || abs (mDiagonal) == n || abs (sDiagonal) == n) return player; return 0 ; } };
给你一个字符串 s 和一个整数 k ,请你找出 s 中的最长子串, 要求该子串中的每一字符出现次数都不少于 k 。返回这一子串的长度。
示例 1:
输入:s = "aaabb" , k = 3 输出:3 解释:最长子串为 "aaa" ,其中 'a' 重复了 3 次。
示例 2:
输入:s = "ababbc" , k = 2 输出:5 解释:最长子串为 "ababb" ,其中 'a' 重复了 2 次, 'b' 重复了 3 次。
提示:
1 <= s.length <= 104s 仅由小写英文字母组成1 <= k <= 105
C++ class Solution {public : int longestSubstring (string s, int k) vector<int > count (26 , 0 ) ; int res = 0 ; for (int i = 0 ; i < s.size (); i ++){ fill (count.begin (), count.end (), 0 ); for (int j = i; j < s.size (); j ++){ count[s[j] - 'a' ] ++; int minK = 1e8 ; for (auto e : count){ if (!e) continue ; minK = min (minK, e); } if (minK >= k) res = max (res, j - i + 1 ); } } return res; } };
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
0 <= i, j, k, l < nnums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
示例 1:
输入:nums1 = [1 ,2 ], nums2 = [-2 ,-1 ], nums3 = [-1 ,2 ], nums4 = [0 ,2 ] 输出:2 解释: 两个元组如下: 1. -> nums1 [0 ] + nums2 [0 ] + nums3 [0 ] + nums4 [1 ] = 1 + + + 2 = 0 2. -> nums1 [1 ] + nums2 [1 ] + nums3 [0 ] + nums4 [0 ] = 2 + + + 0 = 0
示例 2:
输入:nums1 = [0 ], nums2 = [0 ], nums3 = [0 ], nums4 = [0 ] 输出:1
提示:
n == nums1.lengthn == nums2.lengthn == nums3.lengthn == nums4.length1 <= n <= 200-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228
C++ class Solution {public : int fourSumCount (vector<int >& nums1, vector<int >& nums2, vector<int >& nums3, vector<int >& nums4) map<int ,int > AB; map<int ,int > CD; for (auto e1: nums1){ for (auto e2: nums2){ AB[e1 + e2] ++; } } int res = 0 ; for (auto e3: nums3){ for (auto e4: nums4){ if ( AB.count (- e3 - e4)) res += AB[- e3 - e4]; } } return res; } };