中位数贪心合集

中位数贪心

1. [1,10,2,9] ,在一次操作中你可以使数组中的一个元素+1或-1,返回使所有数组元素相等需要的最小操作数 // 目标数为数组中位数

2. 有数组a[n] 求x. 令所有｜x - a[i]｜的和最小, 则 x = a[n/2]

462. 最小操作次数使数组元素相等 II

给你一个长度为 n 的整数数组 nums ，返回使所有数组元素相等需要的最小操作数。

在一次操作中，你可以使数组中的一个元素加 1 或者减 1 。

示例 1：

输入：nums = [1,2,3]
输出：2
解释：
只需要两次操作（每次操作指南使一个元素加 1 或减 1）：
[1,2,3]  =>  [2,2,3]  =>  [2,2,2]

示例 2：

输入：nums = [1,10,2,9]
输出：16

提示：

• n == nums.length
• 1 <= nums.length <= 105
• -109 <= nums[i] <= 109

C++

// nth_element(数组名,数组名+第k小元素,数组名+元素个数) 可以在给定区间内部排序，使得指定元素处于指定位置
class Solution {
public:
    int minMoves2(vector<int>& nums) {
        nth_element(nums.begin(), nums.begin() + nums.size()/ 2, nums.end());
        int target = nums[nums.size()/ 2], res = 0; // 让第k小的元素在第k位上
        for(auto e : nums){
            res += abs(e - target);
        }
        return res;
    }
};

2033. 获取单值网格的最小操作数

给你一个大小为 m x n 的二维整数网格 grid 和一个整数 x 。每一次操作，你可以对 grid 中的任一元素 加 x 或 减 x 。

单值网格 是全部元素都相等的网格。

返回使网格化为单值网格所需的 最小 操作数。如果不能，返回 -1 。

示例 1：

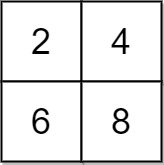
输入：grid = [[2,4],[6,8]], x = 2
输出：4
解释：可以执行下述操作使所有元素都等于 4 ： 
- 2 加 x 一次。
- 6 减 x 一次。
- 8 减 x 两次。
共计 4 次操作。

示例 2：

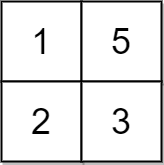
输入：grid = [[1,5],[2,3]], x = 1
输出：5
解释：可以使所有元素都等于 3 。

示例 3：

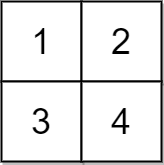
输入：grid = [[1,2],[3,4]], x = 2
输出：-1
解释：无法使所有元素相等。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= x, grid[i][j] <= 104

C++

class Solution {
public:
    int minOperations(vector<vector<int>>& grid, int x) {
        vector<int> res;
        for(auto e: grid)
            for(auto el : e)
                res.emplace_back(el);

        nth_element(res.begin(), res.begin() + res.size()/ 2, res.end());
        int target = res[res.size()/ 2], cnt = 0;
        for(auto e: res)
            if(abs(target - e) % x) return -1;
            else cnt += abs(target - e) / x;
        return cnt;
    }
};