51.N皇后

51. N 皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

• 1 <= n <= 9

C++

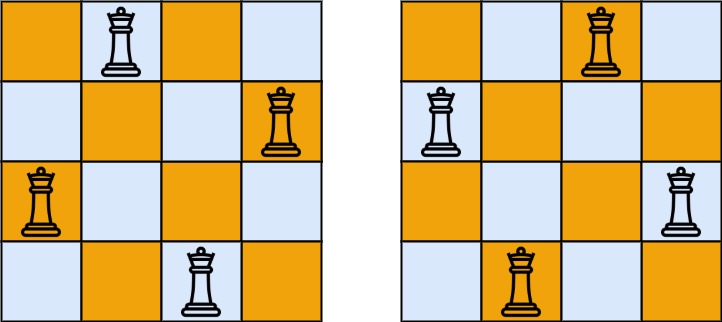
class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        unordered_set<int> columns, diagonals1, diagonals2;
        vector<vector<string>> solutions;
        vector<int> queens(n, -1);
        backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
        return solutions;
    }

    void backtrack(vector<vector<string>> &solutions, vector<int> &queens, int n, int row, unordered_set<int> &columns, unordered_set<int> &diagonals1, unordered_set<int> &diagonals2) {
        if (row == n) {
            vector<string> board = generateBoard(queens, n);
            solutions.push_back(board);
            return;
        } 
            
        for (int i = 0; i < n; i++) {
            int diagonal1 = row - i, diagonal2 = row + i; 
            if (columns.find(i) != columns.end()) continue;
            if (diagonals1.find(diagonal1) != diagonals1.end()) continue;
            if (diagonals2.find(diagonal2) != diagonals2.end()) continue;
            
            queens[row] = i; // 在 row 这行选了 i 列
            columns.insert(i);
            diagonals1.insert(diagonal1);
            diagonals2.insert(diagonal2);
            backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
            queens[row] = -1;
            columns.erase(i);
            diagonals1.erase(diagonal1);
            diagonals2.erase(diagonal2);
        }
    }

    vector<string> generateBoard(vector<int> &queens, int n) {
        vector<string> board;
        for (int i = 0; i < n; i++) {
            string row = string(n, '.');
            row[queens[i]] = 'Q';
            board.push_back(row);
        }
        return board;
    }
};