1463.摘樱桃II

1463. 摘樱桃 II

给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。

你有两个机器人帮你收集樱桃，机器人 1 从左上角格子 (0,0) 出发，机器人 2 从右上角格子 (0, cols-1) 出发。

请你按照如下规则，返回两个机器人能收集的最多樱桃数目：

• 从格子 (i,j) 出发，机器人可以移动到格子 (i+1, j-1)，(i+1, j) 或者 (i+1, j+1) 。
• 当一个机器人经过某个格子时，它会把该格子内所有的樱桃都摘走，然后这个位置会变成空格子，即没有樱桃的格子。
• 当两个机器人同时到达同一个格子时，它们中只有一个可以摘到樱桃。
• 两个机器人在任意时刻都不能移动到 grid 外面。
• 两个机器人最后都要到达 grid 最底下一行。

示例 1：

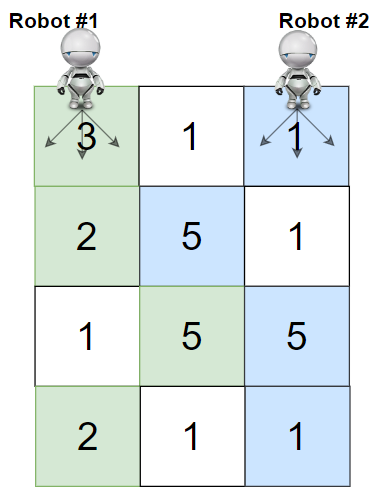
输入：grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
输出：24
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12 。
机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12 。
樱桃总数为： 12 + 12 = 24 。

示例 2：

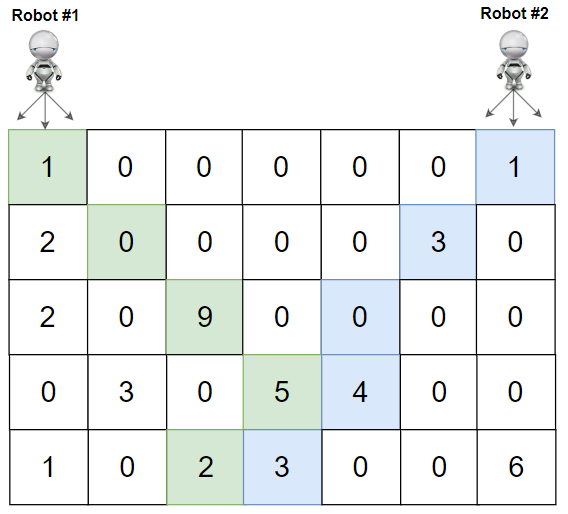
输入：grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
输出：28
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17 。
机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11 。
樱桃总数为： 17 + 11 = 28 。

示例 3：

输入：grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
输出：22

示例 4：

输入：grid = [[1,1],[1,1]]
输出：4

提示：

• rows == grid.length
• cols == grid[i].length
• 2 <= rows, cols <= 70
• 0 <= grid[i][j] <= 100

C++

class Solution {
public:
    int cherryPickup(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        // dp[i][j][k]: 表示1从(0,0)到(i,j)+2从(0,n-1)到(i,k)的最大值
        vector<vector<vector<int>>> dp(m, 
        vector<vector<int>>(n, vector<int>(n, 0)));
        dp[0][0][n - 1] = grid[0][0] + grid[0][n - 1];
        int res = 0;
        for(int i = 1; i < m; i ++) {
            for(int j = 0; j < n; j ++) {
                for(int k = 0; k < n; k ++) {  
                    // 每层的1和2都有活动范围 
                    if(j > i || k < n - 1 - i) continue; 
                    int maxup = 0; 
                    for(auto e1 : {1, 0, -1}) 
                        for(auto e2 : {1, 0, -1})
                            if(j + e1 >= 0 && j + e1 < n && k + e2 >= 0 
                            && k + e2 < n) 
                                maxup = max(maxup, dp[i - 1][j + e1][k + e2]);
                    
                    if(j == k) dp[i][j][k] = maxup + grid[i][j];
                    else dp[i][j][k] = maxup + grid[i][j] + grid[i][k];

                    if(i == m - 1) res = max(res, dp[i][j][k]);
                }
            }
            
        }
        return res;
    } 
};