1335.工作计划的最低难度

1335. 工作计划的最低难度

你需要制定一份 d 天的工作计划表。工作之间存在依赖，要想执行第 i 项工作，你必须完成全部 j 项工作（ 0 <= j < i）。

你每天 至少 需要完成一项任务。工作计划的总难度是这 d 天每一天的难度之和，而一天的工作难度是当天应该完成工作的最大难度。

给你一个整数数组 jobDifficulty 和一个整数 d，分别代表工作难度和需要计划的天数。第 i 项工作的难度是 jobDifficulty[i]。

返回整个工作计划的 最小难度 。如果无法制定工作计划，则返回 -1 。

示例 1：

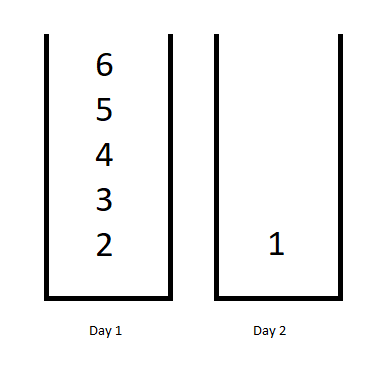
输入：jobDifficulty = [6,5,4,3,2,1], d = 2
输出：7
解释：第一天，您可以完成前 5 项工作，总难度 = 6.
第二天，您可以完成最后一项工作，总难度 = 1.
计划表的难度 = 6 + 1 = 7 

示例 2：

输入：jobDifficulty = [9,9,9], d = 4
输出：-1
解释：就算你每天完成一项工作，仍然有一天是空闲的，你无法制定一份能够满足既定工作时间的计划表。

示例 3：

输入：jobDifficulty = [1,1,1], d = 3
输出：3
解释：工作计划为每天一项工作，总难度为 3 。

示例 4：

输入：jobDifficulty = [7,1,7,1,7,1], d = 3
输出：15

示例 5：

输入：jobDifficulty = [11,111,22,222,33,333,44,444], d = 6
输出：843

提示：

• 1 <= jobDifficulty.length <= 300
• 0 <= jobDifficulty[i] <= 1000
• 1 <= d <= 10

C++

class Solution {
public:
    int minDifficulty(vector<int>& jobDifficulty, int d) {
        int n = jobDifficulty.size();
        if(n < d) return -1;
        // dp[i][j]: 第i天时完成 jobDifficulty[j] 的最大难度  j >= i
        vector<vector<int>> dp(d, vector<int>(n, 1e9)); 

        for(int j = 0; j < n; j ++)  // 初始化第0天完成 0 ～ n - 1 个任务的最大难度
            dp[0][j] = *max_element(jobDifficulty.begin(), jobDifficulty.begin() + j + 1);

        for(int i = 1; i < d; i ++) {
            for(int j = i; j < n; j ++) {
                for(int k = i - 1; k < j; k ++) {
                    // jobDifficulty[k + 1] ～ jobDifficulty[j]
                    int maxNum = *max_element(jobDifficulty.begin() + k + 1, 
                    jobDifficulty.begin() + j + 1); // *max_element 为 [ , )
                    dp[i][j] = min(dp[i - 1][k] + maxNum, dp[i][j]);
                }
            }
        }
        return dp[d - 1][n - 1] >= 1e9 ? -1 : dp[d - 1][n - 1];
    }
};