979.在二叉树中分配硬币

979. 在二叉树中分配硬币

给你一个有 n 个结点的二叉树的根结点 root ，其中树中每个结点 node 都对应有 node.val 枚硬币。整棵树上一共有 n 枚硬币。

在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。移动可以是从父结点到子结点，或者从子结点移动到父结点。

返回使每个结点上 只有 一枚硬币所需的 最少 移动次数。

示例 1：

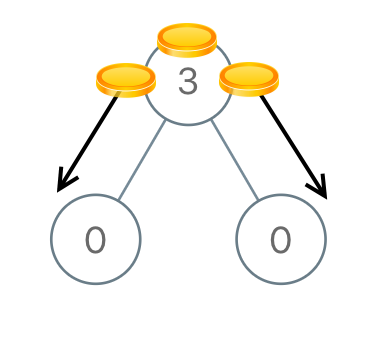
输入：root = [3,0,0]
输出：2
解释：一枚硬币从根结点移动到左子结点，一枚硬币从根结点移动到右子结点。

示例 2：

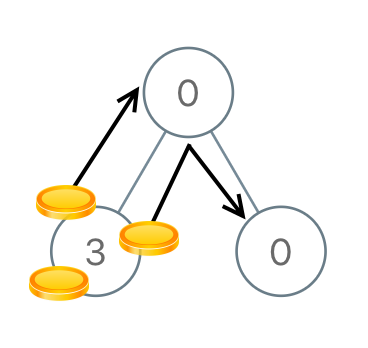
输入：root = [0,3,0]
输出：3
解释：将两枚硬币从根结点的左子结点移动到根结点（两次移动）。然后，将一枚硬币从根结点移动到右子结点。

提示：

• 树中节点的数目为 n
• 1 <= n <= 100
• 0 <= Node.val <= n
• 所有 Node.val 的值之和是 n

C++

/**
* 从后序遍历的第一个叶子节点开始，假设自己有x个金币，剩余x-1个金币都还给父节点，x-1可能为负数、0、正数
* x-1 < 0说明不够金币，需要从父节点获得，因此子节点有|x-1|个入方向的操作，次数加上|x-1|
* x-1 == 0说明刚好，无需与父节点有金币的交换，次数加0
* x-1 > 0 说明有多余的金币，需要交给父节点，因此子节点有x-1个出方向的操作，次数加上|x-1|
*/
class Solution {
public:
    int res = 0;
    int distributeCoins(TreeNode* root) {
        postorder(root);
        return res;
    }

    int postorder(TreeNode* root) {
        if(!root) return 0;

        if(root -> left != nullptr)  root->val += postorder(root -> left);
        if(root -> right != nullptr) root->val += postorder(root -> right);

        res += abs(root -> val - 1);

        return root -> val - 1;
    }
};